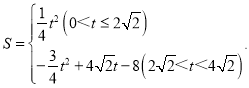Question

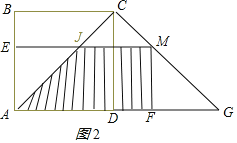
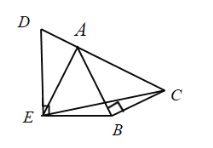
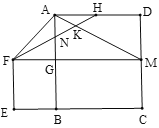
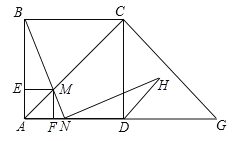
【题目】如图，在边长为2的正方形ABCD中，G是AD延长线上的一点，且DG=AD，动点M从A点出发，以每秒1个单位的速度沿着A→C→G的路线向G点匀速运动(M不与A，G重合)，设运动时间为t秒，连接BM并延长交AG于N．

（1）当AM=_____________时，△ABM是以AB为底边的等腰三角形；

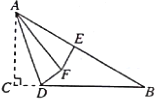
（2）当点N在AD边上时，若BN⊥HN，NH交∠CDG的平分线于H，求证：BN=HN；

（3）过点M分别作AB，AD的垂线，垂足分别为E，F，矩形AEMF与△ACG重叠部分的面积为S，求S与t的函数关系式，并求S最大值．

Answer 1

【答案】（1）；（2）证明见解析；（3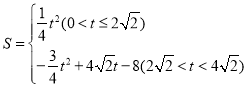），当t=时，S的最大值是．

【解析】

（1）△ABM是以AB为底边的等腰三角形，则为正方形的对角线的交点，从而可得答案，

（2）在AB上截取AK=AN，连接KN；由正方形的性质得出∠ADC=90°，AB=AD，∠CDG=90°，得出BK=DN，先证出∠BKN=∠NDH，再证出∠ABN=∠DNH，由ASA证明△BNK≌△NHD，得出BN=NH即可；

（3）①当M在AC上时，即0＜t≤时，△AMF为等腰直角三角形，得出AF=FM= 求出S=AFFM=；当t=时，即可求出S的最大值； ②当M在CG上时，即＜t＜时，先证明△ACD≌△GCD，得出∠ACD=∠GCD=45°，求出∠ACM=90°，证出△MFG为等腰直角三角形，得出FG=MGcos45°=，得出S=S△ACG-S△CMJ-S△FMG．

解：（1）△ABM是以AB为底边的等腰三角形，

此时点M为AC的中点，

正方形ABCD，

故答案为：

（2）在AB上截取AK=AN，连接KN；

正方形ABCD，

∠ADC=90°，AB=AD，∠CDG=90°，

BK=DN，

平分

△BNK≌△NHD，

BN=NH；

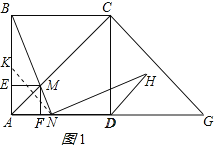
（3）①当点M在AC上时，即0＜t≤时，

由正方形的性质得：△AMF为等腰直角三角形．

∵AM=t，

∴AF=FM=

∴S=AFFM=

当时，

当点M在CG上时，

即＜t＜时，CM=，MG=．

∵AD=DG，∠ADC=∠CDG，CD=CD，

∴△ACD≌△GCD（SAS），

∴∠ACD=∠GCD=45°

∴∠ACM=∠ACD+∠GCD=90°

∴∠G=90-∠GCD=90°-45°=45°

∴△MFG为等腰直角三角形．

∴FG=，

∴S=S△ACG-S△MCJ-S△FMG=

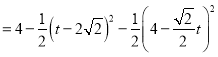
当 ，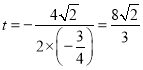

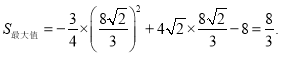
综上：当

∴