题目内容
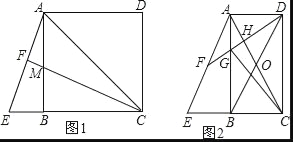
【题目】已知四边形ABCD是矩形,连接AC,点E是边CB延长线上一点,CA=CE,连接AE,F是线段AE的中点,
(1)如图1,当AD=DC时,连接CF交AB于M,求证:BM=BE;
(2)如图2,连接BD交AC于O,连接DF分别交AB、AC于G、H,连接GC,若∠FDB=30°,S四边形GBOH=![]() ,求线段GC的长.
,求线段GC的长.
【答案】(1)见解析;(2)![]()
【解析】分析:(1)如图1,根据等腰三角形的三线合一得CF⊥AE,则∠AFC=90°,证明△AEB≌△CMB,可得BE=BM;
(2)如图2,作辅助线构建三角形全等,先证明△AMF≌△EBF,得FM=BF,AM=BE,再证明△DMB是等腰三角形,由三线合一得:DF平分∠BDM,根据∠FDB=30°得△BDM是等边三角形;由此△ACE为等边三角形,△OHD为直角三角形,设未知数:OH=x,根据S四边形GBOH=S△DGB-S△OHD,列方程得出结论.
详解:(1)如图1,∵AC=EC,F是AE的中点,
∴CF⊥AE,
∴∠AFC=90°,
∵四边形ABCD是矩形,AD=DC,
∴矩形ABCD为正方形,
∴AB=BC,∠ABC=90°,
∴∠AFC=∠ABC,
∵∠AMF=∠BMC,
∴∠EAB=∠MCB,
∵∠ABE=∠ABC=90°,
∴△AEB≌△CMB,
∴BE=BM;
(2)如图2,连接BF并延长交直线AD于M,
∵F是AE的中点,
∴AF=EF,
∵四边形ABCD是矩形,
∴AD∥BC,AC=BD,
∴∠M=∠FBE,
∵∠AFM=∠EFB,
∴△AMF≌△EBF,
∴FM=BF,AM=BE,
∵AD=BC,
∴AD+AM=BC+BE,
即DM=CE,
∵AC=CE,
∴EC=DM=AC=BD,
∴△DMB是等腰三角形,
∵F是BM的中点,
∴DF平分∠BDM,
∵∠BDF=30°,
∴∠BDM=60°,
∴△BDM是等边三角形,
∴∠M=60°,
在Rt△BCD中,∠BDC=90°﹣60°=30°,
∴∠DBC=60°,
∵OB=OC,
∴∠DBC=∠OCB=60°,
∴△ACE为等边三角形,
在△OHD中,∠HOD=∠BOC=60°,
∴∠OHD=90°,
设OH=x,则OD=2x,BD=4x,BC=2x,
∴DH=![]() x,AH=x,DC=AB=2
x,AH=x,DC=AB=2![]() x,
x,
Rt△ABC中,∠ACE=60°,
∴∠BAC=30°,
∴cos30°=![]() ,
,
AG=![]() =
=![]() ,
,
∴BG=AB﹣AG=2![]() x﹣
x﹣![]() =
=![]() ,
,
∴S四边形GBOH=S△DGB﹣S△OHD,
=![]() BGAD﹣
BGAD﹣![]() OHDH,
OHDH,
=![]()
![]() 2x﹣
2x﹣![]() x
x![]() x=
x=![]() ,
,
解得:x2=9,
x=±3,
∴BC=2x=6,
BG=![]() ×3=4
×3=4![]() ,
,
由勾股定理得:CG=![]() =
=![]() =2
=2![]() .
.