��Ŀ����
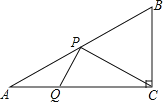
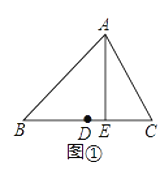
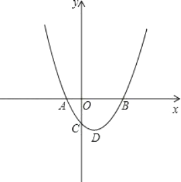
����Ŀ����ͼ��������y=x2��4x��1����ΪD����x���ཻ��A��B���㣬��y���ཻ�ڵ�C��
��1�������������ߵĶ���D�����ꣻ
��2�������㣨0��4������x��ƽ�е�ֱ����������y=x2��4x��1�ཻ��M��N���㣨M��N����ࣩ����MNΪֱ������P������D����P�����ߣ��е�ΪE�����DE�ij���
��3������ƽ�ƣ�2���е�ֱ��MN����MNΪֱ���ġ�P�ܷ���x�����У�����ܹ��������P�İ뾶��������ܣ���˵�����ɣ�
���𰸡���1����D������Ϊ��2��-5������2��DE=6![]() ����3���ܹ����У����ɼ�����.
����3���ܹ����У����ɼ�����.
��������
��1�������䷽�����ɽ���������ʽ����Ϊ��y=��x-2��2-5���ɶ���ʽ����������������ߵĶ���D�����ꣻ
��2���ɾ����㣨0��4������x��ƽ�е�ֱ����������y=x2-4x-1�ཻ��M��N���㣨M��N����ࣩ���������M��N�����꣬�������P�����꣬Ȼ�����PE��PD�ij����������ߵ����ʣ��ɹ��ɶ����������DE�ij���
��3��������֪���ɵõ�P�ĺ�����Ϊ2��������MNΪֱ���ġ�P��x�����У��ɵ������߹��㣨2+r��r����2+r��-r�������������������ʽ�������r��ֵ�����֤����MNΪֱ���ġ�P����x�����У�
��1����y=x2-4x-1=x2-4x+4-5=��x-2��2-5��
���D��������2��-5����
��2���ߵ�y=4ʱ��x2-4x-1=4��
���x=-1��x=5��
��M������-1��4������N������5��4����
��MN=6��P�İ뾶Ϊ3����P������Ϊ��2��4����
����PE����PE��DE��
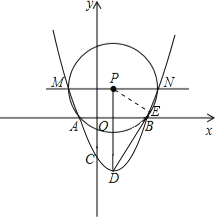
��PD=9��PE=3��
���ݹ��ɶ�����DE=6![]() ��
��
��3���ܹ����У�
���ɣ����P�İ뾶Ϊr�����������ߵĶԳ��ԣ������߹��㣨2+r��r����2+r��-r����
���������߽���ʽ�ã���2+r��2-4��2+r��-1=r��
���r=![]() ��r=
��r=![]() ����ȥ����
����ȥ����
�ѣ�2+r��-r�����������ߵã���2+r��2-4��2+r��-1=-r��
��ã�r=![]() ����r=
����r=![]() ����ȥ����
����ȥ����