Question

【题目】如图，四边形ABCD各个顶点的坐标分别为A（﹣2，8），B（﹣11，6），C（﹣14，0），D（0，0）．

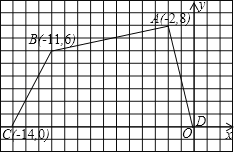
（1）求这个四边形的面积；

（2）如果把四边形ABCD各个顶点的纵坐标保持不变，横坐标增加4，所得的四边形的面积又是多少？

Answer 1

【答案】（1）80；（2）还是80

【解析】

（1）过点A、B分别作x轴的垂线，把四边形ABCD分成两个直角三角形和一个梯形，然后根据三角形的面积公式与梯形的面积公式列式计算即可得解；

（2）根据平移变换只改变图形的位置不改变图形的形状与大小可知所得四边形的面积与原四边形ABCD的面积相等．

解：（1）过点A作AF⊥x轴，过点B作BE⊥x轴，如图：

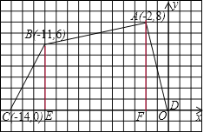
则DF＝2，CE＝3，AF＝8，BE＝6，EF＝﹣2﹣（﹣11）＝9，

四边形ABCD的面积＝S△ADF+S△BCE+S梯形ABEF，

，

，

；

（2）四边形ABCD各个顶点的纵坐标保持不变，横坐标增加4，

就是把四边形ABCD向右平移4个单位，

所以，所得的四边形的面积不变，还是80．

故答案是：（1）80；（2）还是80