题目内容
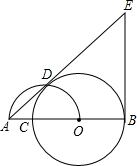
如图:有一轴截面为正三角形的圆锥形容器,内部盛水高度为10cm,放入一个球后,水面恰好与球相切,求球的半径.(圆锥的体积公式V=
πR2h,其中R为底面半径,h为高线;球的体积公式V=
πR3,其中R为球的半径)
| 1 |
| 3 |
| 4 |
| 3 |

如图所示,则△ABS为等边三角形,
∵SG=h=10,DG=
×10=
,
∴V水=
•DG2•SG=
h3.
设铁球的半径为R,
则SO=2R,SG=3R,
在Rt△FSB中,DG=SGtan∠FSB=
R,
设放入球之后,球与水共占体积为V′,
则V′=
•(DG)2•SG=
(
R)2•3R=3πR3,V球=
R3.
依题意,有V′=V球+V水,
即3πR3=
πR3+
h3,
∴R=
×10=
,
答:铁球的半径为
.
∵SG=h=10,DG=
| ||
| 3 |
10
| ||
| 3 |
∴V水=
| π |
| 3 |
| π |
| 9 |

设铁球的半径为R,
则SO=2R,SG=3R,
在Rt△FSB中,DG=SGtan∠FSB=
| 3 |
设放入球之后,球与水共占体积为V′,
则V′=
| π |
| 3 |
| π |
| 3 |
| 3 |
| 4π |
| 3 |
依题意,有V′=V球+V水,
即3πR3=
| 4 |
| 3 |
| π |
| 9 |
∴R=
| |||
| 15 |
2
| |||
| 3 |
答:铁球的半径为
2
| |||
| 3 |

练习册系列答案
相关题目