题目内容
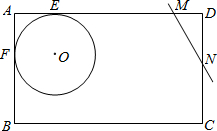
如图,矩形ABCD的边AD、AB分别与⊙O相切于E、F,AE=
.
(1)求弧EF的长.
(2)若AD=
+5,直线MN分别交DA、DC于点M、N,∠DMN=60°,将直线MN沿射线DA方向平移,当MN和⊙O第一次相切时,求点D到直线MN的距离.
(3)若点D到直线MN的距离为4时,请直接写出⊙O和直线MN的位置关系.
| 3 |
(1)求弧EF的长.
(2)若AD=
| 3 |
(3)若点D到直线MN的距离为4时,请直接写出⊙O和直线MN的位置关系.

(1)连接OE、OF.
∵AD、AB与⊙O相切于E、F,
∴OE⊥AD,OF⊥AB
∵矩形ABCD中,∠A=90°,
∴四边形OEAF是矩形.
∵OE=OF,
∴四边形OEAF是正方形,
∴OE=OF=AE=
,∠O=90°,
∴弧EF的长为:
=
;
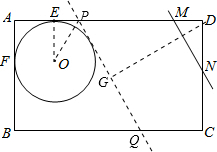 (2)当MN和⊙O第一次相切时,设MN交AD于P,交BC于Q,连接OP,OE,过D作DG⊥MN于G.
(2)当MN和⊙O第一次相切时,设MN交AD于P,交BC于Q,连接OP,OE,过D作DG⊥MN于G.
∵MN∥PQ,
∴∠DMN=∠DPQ=60°,
∴∠APQ=120°.
∵PA和PQ与⊙O相切,
∴∠EPO=∠OPQ=60°.
在△OEP中,∠OEP=90°,∠EOP=30°,OE=
,
∴EP=1,OP=2,
∴DP=AD-AE-EP=
+5-
-1=4.
在△DPG中,∵∠DGP=90°,∠PDG=30°,
∴DG=PD•cos30°=2
,
∴点D到直线MN的距离d为2
;
(3)设点D到直线MN的距离为d.
由(2)知,当d=2
时,直线MN与⊙O第一次相切,
∵⊙O的半径为
,∴当d=4
时,直线MN与⊙O第二次相切,
又∵2
<4<4
,
∴当d=4时,MN直线与⊙O相交.

∵AD、AB与⊙O相切于E、F,
∴OE⊥AD,OF⊥AB
∵矩形ABCD中,∠A=90°,
∴四边形OEAF是矩形.
∵OE=OF,
∴四边形OEAF是正方形,
∴OE=OF=AE=
| 3 |
∴弧EF的长为:
90π×
| ||
| 180 |
| ||
| 2 |
 (2)当MN和⊙O第一次相切时,设MN交AD于P,交BC于Q,连接OP,OE,过D作DG⊥MN于G.
(2)当MN和⊙O第一次相切时,设MN交AD于P,交BC于Q,连接OP,OE,过D作DG⊥MN于G.∵MN∥PQ,
∴∠DMN=∠DPQ=60°,
∴∠APQ=120°.
∵PA和PQ与⊙O相切,
∴∠EPO=∠OPQ=60°.
在△OEP中,∠OEP=90°,∠EOP=30°,OE=
| 3 |
∴EP=1,OP=2,
∴DP=AD-AE-EP=
| 3 |
| 3 |
在△DPG中,∵∠DGP=90°,∠PDG=30°,
∴DG=PD•cos30°=2
| 3 |
∴点D到直线MN的距离d为2
| 3 |
(3)设点D到直线MN的距离为d.
由(2)知,当d=2
| 3 |
∵⊙O的半径为
| 3 |
| 3 |
又∵2
| 3 |
| 3 |
∴当d=4时,MN直线与⊙O相交.


练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目