题目内容
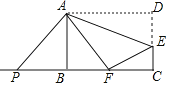
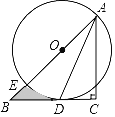
【题目】如图,在![]() 中,∠C=90°,AC=BC,点O在AB上,以O为圆心,OA为半径作⊙O,与BC相切于点D,且交AB于点E.
中,∠C=90°,AC=BC,点O在AB上,以O为圆心,OA为半径作⊙O,与BC相切于点D,且交AB于点E.
(1)连结AD,求证:AD平分∠CAB;
(2)若BE=![]() ﹣1,求阴影部分的面积.
﹣1,求阴影部分的面积.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接OD,证OD∥AC,求出∠OAD=∠ODA=∠CAD即可;
(2)证明△BOD是等腰直角三角形,分别求出△BOD和扇形EOD的面积即可.
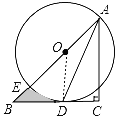
(1)证明:如图,连结OD,
∵⊙O与BC相切于点D,
∴OD⊥BC,
即∠ODB=90°.
又∵∠C=90°,
∴OD∥AC,
∴∠ODA=∠CAD.
在⊙O中,OA=OD,
∴∠ODA=∠OAD,
∴∠OAD=∠CAD,
∴AD平分∠CAB.
(2)解:在Rt△ABC中,∠C=90°,AC=BC,
∴∠B=45°,
∴∠BOD=45°,
∴△BOD是等腰直角三角形,
∴OB=![]() OD,BD=OD,
OD,BD=OD,
设⊙O的半径为r,则OD=BD=r,![]() ,
,
∴![]() ,
,
∴r=1,
∴![]() =
=![]() .
.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目