��Ŀ����
����Ŀ���ҹ�������ѧ�һ���˵������ȱ��ʱ��ֱ�ۣ�������ʱ�����������ν���ǽ����ѧ�������Ҫ˼�뷽��.���磬����ʽ![]() �ļ���������������
�ļ���������������![]() ����Ӧ�ĵ���2����Ӧ�ĵ�֮��ľ��룻��Ϊ
����Ӧ�ĵ���2����Ӧ�ĵ�֮��ľ��룻��Ϊ![]() ������
������![]() �ļ����������������
�ļ����������������![]() ����Ӧ�ĵ���
����Ӧ�ĵ���![]() ����Ӧ�ĵ�֮��ľ�����
����Ӧ�ĵ�֮��ľ�����
��. �������⣺����ʽ![]() ����Сֵ�Ƕ��٣�
����Сֵ�Ƕ��٣�
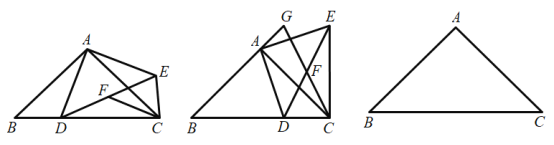
��. ̽�����⣺��ͼ����![]() �ֱ��ʾ����
�ֱ��ʾ����![]() ��
��![]() ��
��
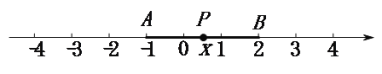
��![]() �ļ����������߶�
�ļ����������߶�![]() ��
��![]() �ij���֮��
�ij���֮��
�൱��![]() ���߶�
���߶�![]() ��ʱ��
��ʱ��![]() ;�����
;�����![]() �ڵ�
�ڵ�![]() �������
�������![]() ���Ҳ�ʱ
���Ҳ�ʱ ![]()
��![]() ����Сֵ��3��
����Сֵ��3��
��.������⣺
��.![]() ����Сֵ�� ��
����Сֵ�� ��
��.��������˼�뷽���ⲻ��ʽ��![]()
![]()
��.��![]() Ϊ��ֵʱ������ʽ
Ϊ��ֵʱ������ʽ![]() ����Сֵ��2��
����Сֵ��2��
���𰸡���6����![]() ��
��![]() ����
����![]() ��
��![]()
��������
(3)�ٸ��ݾ���ֵ�ļ��������֪����������ϵĵ㵽-2�ľ���͵�4�ľ���֮�͵���Сֵ��
�ڸ������⻭����Ӧ��ͼ�Σ�ȷ��������ʽ�Ľ⼯���ɣ�
�۸���ԭʽ����СֵΪ2���õ�3��ߺ��ұߣ��ҵ�3����Ϊ2�ĵ㼴�ɣ�
�⣺(3)����A��ʾ����Ϊ4��B��ʾ����Ϊ-2��P��ʾ����Ϊx��
��![]() ��ʾ�����ϵĵ�P��4�ľ��룬���߶�PA��ʾ��
��ʾ�����ϵĵ�P��4�ľ��룬���߶�PA��ʾ��
![]() ��ʾ�����ϵĵ�P��-2�ľ��룬���߶�PB��ʾ��
��ʾ�����ϵĵ�P��-2�ľ��룬���߶�PB��ʾ��
��![]() �ļ��������ʾΪPA+PB����P���߶�AB��ʱȡ����СֵΪAB��
�ļ��������ʾΪPA+PB����P���߶�AB��ʱȡ����СֵΪAB��
���߶�AB�ij���Ϊ6��
��![]() ����СֵΪ6.
����СֵΪ6.
�ʴ�Ϊ��6.
����A��ʾ-3��B��ʾ1��P��ʾx��
���߶�AB�ij���Ϊ4����
![]() �ļ��������ʾΪPA+PB��
�ļ��������ʾΪPA+PB��
������ʽ�ļ���������PA+PB��AB��
��P�������߶�AB�ϣ�Ӧ����A��������B���Ҳ࣬
������ʽ�Ľ⼯Ϊ![]() ��
��![]() ��
��
�ʴ�Ϊ��![]() ��
��![]() ��
��
����A��ʾ-a��B��ʾ3��P��ʾx��
���߶�AB�ij���Ϊ![]() ��
��
![]() �ļ��������ʾΪPA+PB����P���߶�AB��ʱPA+PBȡ����Сֵ��
�ļ��������ʾΪPA+PB����P���߶�AB��ʱPA+PBȡ����Сֵ��
��![]()
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
�ʴ�Ϊ��![]() ��
��![]() .
.

 ���źþ���Ԫ����ĩ��ϵ�д�
���źþ���Ԫ����ĩ��ϵ�д�