Question

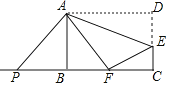
【题目】如图，矩形ABCD中，AB＝12，AD＝15，E是CD上的点，将△ADE沿折痕AE折叠，使点D落在BC边上点F处，点P是线段CB延长线上的动点，连接PA，若△PAF是等腰三角形，则PB的长为____．

Answer 1

【答案】6或9或12.5．

【解析】

分若AP=AF；PF=AF以及AP=P三种情形分别讨论求出满足题意的PB的值即可。

解：∵四边形ABCD是矩形，

由折叠对称性：AF＝AD＝15，FE＝DE．

在Rt△ABF中，BF＝9，

∴FC＝6，

分三种情形讨论：

若AP＝AF，

∵AB⊥PF，

∴PB＝BF＝9，

若PF＝AF，则PB+9＝15，

解得PB＝6，

若AP＝PF，在Rt△APB中，AP2＝PB2+AB2，解得PB＝12.5，

综合得PB＝6或9或12.5．

故答案为：6或9或12.5．