Question

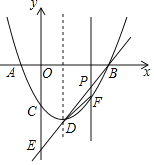
【题目】如图，已知在Rt△ABC中，∠ACB＝90°，BD是△ABC的角平分线，E是AB上一点，且AE＝AD，连接ED，作EF⊥BD于F，连接CF．则下面的结论：

①CD＝CF；

②∠EDF＝45°；

③∠BCF＝45°；

④若CD＝4，AD＝5，则S△ADE＝10．其中正确结论的个数是（　　）

A. 1个B. 2个C. 3个D. 4个

Answer 1

【答案】C

【解析】

首先证明∠EDF=45°再利用全等三角形的性质以及圆周角定理、角平分线的性质定理一一判断即可．

∵AD=AE，

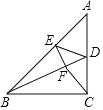
∴∠ADE=∠AED，
∵∠AED=∠ABD+∠BDE，
∴2∠ABD+2∠BDE+∠A=180°，
∵BD平分∠ABC，
∴∠ABC=2∠ABD，
∵∠ACB=90°，
∴∠A+∠ABC=90°，
∴2∠BDE=90°，
∴∠BDE=45°，
∵EF⊥DF，
∴∠EFD=90°，
∴∠EDF=∠FED=45°，故②正确，
延长EF交BC于H，连接CD．

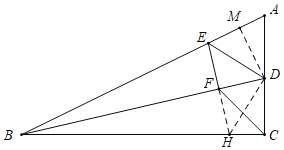
∵∠FBE=∠FBH，BF=BF，∠BFE=∠BFH，
∴△BFE≌△BFH（ASA），
∴EF=FH，∵DF⊥EH，
∴DE=DH，
∴∠DEH=∠DHE=45°，
∵∠DFH+∠DCH=180°，
∴D，F，H，C四点共圆，
∴∠DCF=∠DHF=45°，
∴∠BCF=45°，故③正确，
作DM⊥AB于M，
∵BD平分∠ABC，DC⊥BC，DM⊥AB，
∴DM=DC=4，
∵AE=AD=5，
∴S△ADE=AEDM=10，故④正确，
无法判断CF≠CD，故①错误，
故选：C．