��Ŀ����
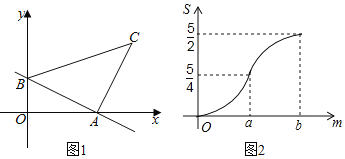
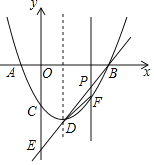
����Ŀ����ͼ���Գ���Ϊֱ��x=1��������y=x2��bx+c��x�ύ��A��x1��0����B��x2��0����x1��x2�����㣬��y�ύ��C�㣬��![]() +
+![]() =��
=��![]() ��
��
��1���������ߵĽ���ʽ��
��2�������߶���ΪD��ֱ��BD��y����E�㣻
�����PΪ�߶�BD��һ�㣨��P����B��D�����غϣ�������P��x��Ĵ����������߽��ڵ�F������BDF��������ֵ��
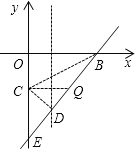
�����߶�BD���Ƿ���ڵ�Q��ʹ�á�BDC=��QCE�������ڣ������Q�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1�������߽���ʽΪ��y=x2��2x��3����2���ٵ�a=2ʱ��S���=��4+8��3=1���ڴ��ڵ�Q����Ϊ��![]() ����3��
����3��
����������1��Ӧ�öԳ��᷽�̡�����ϵ����ϵ��b��c
��2���������P�����ʾ��BDF����������ֵ��
�����ù��ɶ����涨����֤����BDC=90������QC��y�ᣬ����ɽ⣮
��1���������߶Գ���Ϊֱ��x=1
��-![]() ��1
��1
��b=2
��һԪ���η��̸���ϵ����ϵ��
x1+x2=-![]() ��x1x2=
��x1x2=![]() ��
��
��![]() ��
��
��![]() ��
��
��c=-3��
�������߽���ʽΪ��y=x2-2x-3��
��2���ɣ�1����D����Ϊ��1��-4����
��y=0ʱ��x2-2x-3=0��
���x1=-1��x2=3��
���B������3��0����
�����F������a��b����
���BDF�����S=![]() ����4-b����a-1��+
����4-b����a-1��+![]() ��-b����3-a��-
��-b����3-a��-![]() ��2��4��
��2��4��
������S=2a-b-6��
��b=a2-2a-3��
��S=2a-��a2-2a-3��-6=-a2+4a-3��
��a=-1��0��
�൱a=2ʱ��S���=-4+8-3=1��
�ڴ���.
����֪��D����Ϊ��1��-4������B����Ϊ��3��0����
��ֱ��BD����ʽΪ��y=2x-6��
���E������0��-6����
��BC��CD�����ɹ��ɶ����ã�
CB2=��3-0��2+��-3-0��2=18
CD2=12+��-4+3��2=2��
BD2=��-4��2+��3-1��2=20��
��CB2+CD2=BD2��
���BDC=90�㣬
�ߡ�BDC=��QCE��
���QCE=90�㣬
���Q������Ϊ-3��
����-3=2x-6��
��x=![]() ��
��
����ڵ�Q����Ϊ��![]() ��-3��
��-3��

����Ŀ����ʮһ���ƽ����ڼ䣬���ؾ���������֯�����л���������9��30�յ��ο�����Ϊ1���ˣ������������������ÿ��Ӵ����ο������仯���±���������ʾ��ǰһ����������������ʾ��ǰһ���ٵ���������
���� | 10��1�� | 10��2�� | 10��3�� | 10��4�� | 10��5�� | 10��6�� | 10��7�� |
�����仯 ����λ�����ˣ� |
|
|
|
|
|
|
|
��1������ݼ����ж��������ο��������������죬�ж������ˣ�
��2������9��30�յ��ο�����1����Ϊ����ÿ����Ʊ��Ϊ10Ԫ���ʻƽ����ڼ仴������ƽ��ÿ����Ʊ�����������Ԫ��