题目内容
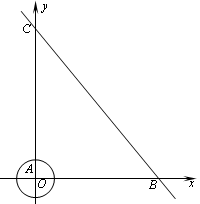
如图,等腰三角形ABC中,AC=BC=3,AB=4.以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E.
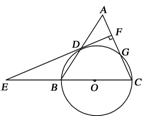
(1)求证:直线EF是⊙O的切线;
(2)连接BG,求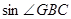 的值.
的值.

(1)求证:直线EF是⊙O的切线;
(2)连接BG,求
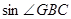 的值.
的值.(1)连接OD,根据圆的基本性质可得∠OBD=∠ODB,再由AC=BC可得∠OBD=∠A,即可得到∠ODB=∠A,从而可得OD//AC,再结合DF⊥AC即可证得结论;(2)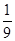
试题分析:(1)连接OD,根据圆的基本性质可得∠OBD=∠ODB,再由AC=BC可得∠OBD=∠A,即可得到∠ODB=∠A,从而可得OD//AC,再结合DF⊥AC即可证得结论;
(2)设CG=x,BC=3,CG=x,
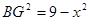 AG=3-x,AB=4,再根据勾股定理即可列方程求解.
AG=3-x,AB=4,再根据勾股定理即可列方程求解.(1)连接OD
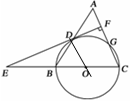
∵OB=OD
∴∠OBD=∠ODB
∵AC=BC
∴∠OBD=∠A
∴∠ODB=∠A
∴OD//AC
∴∠EDO=∠EFC=90°
∴EF为切线;
(2) 设CG=x,BC=3,CG=x,
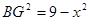 AG=3-x,AB=4
AG=3-x,AB=4由
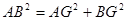 可得
可得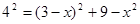 ,解得x=
,解得x=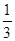 ,
,则sin∠GBC=
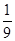 .
.点评:在证明切线的问题中,一般先连接切点与圆心,再证垂直.

练习册系列答案
相关题目
 的圆周角所对的弦是直径; ④不在同一条直线上的三个点确定一个圆;
的圆周角所对的弦是直径; ④不在同一条直线上的三个点确定一个圆;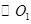 与
与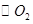 相交于点E、F,点P是两圆连心线上的一点,分别联结PE、PF交
相交于点E、F,点P是两圆连心线上的一点,分别联结PE、PF交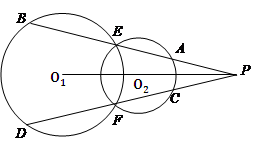
 半径为3cm,⊙
半径为3cm,⊙ 的半径为7 cm,若⊙
的半径为7 cm,若⊙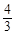 .
.

 ,求AB的长.
,求AB的长.