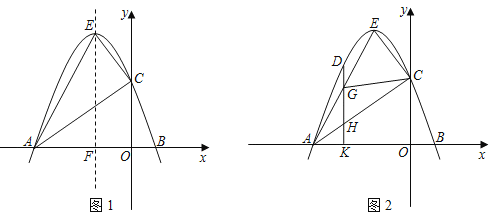题目内容
【题目】用线段EG,FH将正方形ABCD按如图1所示的方式分割成4个全等的四边形,且AE=BF=CG=DH,tan∠HFC=2,再将这四个四边形按如图2所示的方式拼成一个大正方形IJKL,若设正方形ABCD的面积为S1,正方形IJKL的面积为S2.小四边形MNPQ的面积为8,则 ![]() 的值为( )
的值为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
过点H作HH1⊥BC于点H1,设AE=BF=CG=DH=a,AB=CD=BC=AD=b,用含a,b的代数式表示出FH1,H1H,利用解直角三角形求出b=4a,可得到S1;再利用SAS证明△AEH≌△DHG,利用全等三角形的性质,可得到EH=HG,∠AHE=∠DGH,就可推出△EHG是等腰直角三角形,利用解直角三角形可得到EG=![]() EH,然后由勾股定理就可求出正方形IJKL的边长,利用正方形的面积公式求出S2,然后求出两正方形的面积的比值.
EH,然后由勾股定理就可求出正方形IJKL的边长,利用正方形的面积公式求出S2,然后求出两正方形的面积的比值.
过点H作HH1⊥BC于点H1,
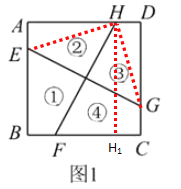
设AE=BF=CG=DH=a,AB=CD=BC=AD=b,
∴FH1=b-2a,H1H=CD=b,
在Rt△H1HF中,
![]() ,
,
∴b=4a,
∴S1=16a2;
∵AH=DG,∠A=∠D=90°,AE=HD,
∴△AEH≌△DHG(SAS),
∴EH=HG,∠AHE=∠DGH,
∵∠DHG+∠DGH=90°=∠DHG+∠AHE,
∴∠EHG=90°,
∴△EHG是等腰直角三角形,
EG=![]() EH,
EH,
在Rt△AEH中,AH=AD-DH=4a-a=3a,
![]() ,
,
∴正方形IJKL的边长为EG=![]() .
.
∴S2=![]() ,
,
∴![]() .
.
故选:C.

 步步高达标卷系列答案
步步高达标卷系列答案【题目】在抗击“新冠肺炎疫情”的日子里,上海全市学生积极响应号召开展“停课不停学”的线上学习活动,某中学为了了解全校1200名学生一周内平均每天进行在家体育锻炼时间的情况,随机调查了该校100名学生一周内平均每天在家体育锻炼时间的情况,结果如下表:
时间(分) | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 |
人数 | 16 | 24 | 14 | 10 | 8 | 6 | 8 | 4 | 6 | 4 |
完成下列各题:
(1)根据上述统计表中的信息,可知这100名学生一周内平均每天在家体育锻炼时间的众数是______分,中位数是_______分;
(2)小李根据上述统计表中的信息,制作了如下频数分布表和频数分布直方图(不完整),那么①频数分布表中m=______,n=______;②请补全频数分布直方图;
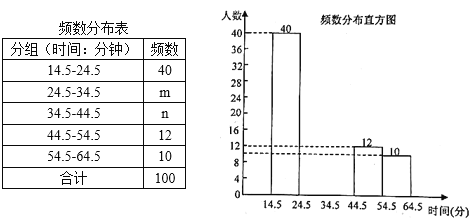
(3)请估计该学校平均每天在家体育锻炼时间不少于35分钟的学生大约有______人.