Question

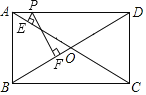
【题目】如图，在矩形ABCD中，AB＝15，AD＝20，P是AD边上不与A和D重合的一个动点，过点P分别作AC和BD的垂线，垂足为E，F，则PEPF的最大值为_____．

Answer 1

【答案】36．

【解析】

设AP＝x，则PD＝20﹣x，通过证△APE∽△ACD，△DPF∽△DBA，分别用含x的代数式将PE，PF表示出来，并算出其乘积，然后用二次函数的性质求出其最大值即可．

在Rt△ABD中，BD＝＝＝25，

∵PE⊥AC，PF⊥BD，四边形ABCD是矩形，

∴∠PEA＝∠CDA＝∠PFD＝∠BAD=90°，AC=BD=25，CD=AB=15，

∵∠PAE＝∠CAD，∠PEA＝∠CDA=90°，

∴△APE∽△ACD，

∴＝＝，

∵∠PDF＝∠BDA，∠PFD=∠BAD=90°，

∴△DPF∽△DBA，

∴＝＝，

设AP＝x，则PD＝20﹣x，

∴PE＝x，PF＝（20﹣x）＝12﹣x，

∴PEPF＝x×（12﹣x）

＝﹣x2+x

＝﹣（x﹣10）2+36.

∴当x＝10时，PEPF有最大值，最大值为36，

故答案为：36