��Ŀ����
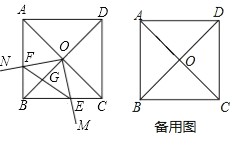
����Ŀ����������ABCD�У�AB��8��AC��BD�ཻ�ڵ�O��
��1����ͼ��������OM���BC�ཻ�ڵ�E��������OM�Ƶ�O˳ʱ����ת90�����õ�����ON������ON���AB�ཻ�ڵ�F������EF��BO�ڵ�G��
��ֱ��д���ı���OEBF�������_______.
����֤����OEF�ǵ���ֱ��������.
����OG��![]() ����OE�ij�.
����OE�ij�.
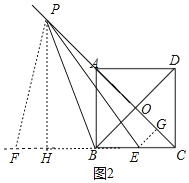
��2����P������CA��һ�㣬��BP��2![]() ������PM��ֱ��BC�ཻ�ڵ�E����CE��2ʱ��������PM�Ƶ�P˳ʱ����ת45�㣬�õ�����PN������PN��ֱ��BC�ཻ�ڵ�F����ֱ��д��BF�ij�________��
������PM��ֱ��BC�ཻ�ڵ�E����CE��2ʱ��������PM�Ƶ�P˳ʱ����ת45�㣬�õ�����PN������PN��ֱ��BC�ཻ�ڵ�F����ֱ��д��BF�ij�________��
���𰸡���1����16����֤������������5����2��![]() ��
��![]() ��
��
��������
��1���ٸ��������ε����ʼ���ת�����ʣ�������ASA����֤��BOF�ա�COE���ɵ�S��BFO��S��CEO��������⣻����ȫ�������ε����ʿɵ�OE��OF�����ɵý��ۣ����������ϵ����S��EFO��![]() ��S�ı���OEBF��
��S�ı���OEBF��![]() ������OE�ij�����2������P��PH��BC��H������E��EG��AC�ڵ�G��������������ۣ��������ε����ʺ��ɶ�������PH��10��ͨ��֤����PFH�ס�PEG���ɵ�
������OE�ij�����2������P��PH��BC��H������E��EG��AC�ڵ�G��������������ۣ��������ε����ʺ��ɶ�������PH��10��ͨ��֤����PFH�ס�PEG���ɵ�![]() ��������⣮
��������⣮
��1���١��ı���ABCD�������Σ�
��AO��BO��CO��AB��BC��8����ABO����BCO��45����BD��AC��
��AC��8![]() ��
��
��OA��OC��OB��4![]() ��
��
�߽�����OM�Ƶ�O˳ʱ����ת90�����õ�����ON��
���FOE��90������BOC��
���FOE-��BOE=��BOC-��BOE������BOF����COE��
����BOF����COE��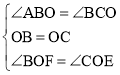 ��
��
���BOF�ա�COE��ASA��
��S��BFO��S��CEO��
���ı���OEBF�������S��OBC��![]() ��4
��4![]() ��4
��4![]() ��16��
��16��
�ʴ�Ϊ16��
�ڡߡ�BOF�ա�COE��
��OE��OF��
�ߡ�EOF��90����
���OEF�ǵ���ֱ��������.
�ۡ�OG��![]() ��OB��4
��OB��4![]() ��
��
��BG��![]() ��
��
��S��BFG��S��FGO��BG��GO��7��25��S��BEG��S��EGO��BG��GO��7��25��
��S��BEF��S��EFO��7��25��
��S�ı���OEBF=16��
��S��EFO��![]() ��S�ı���OEBF��
��S�ı���OEBF��![]() ��
��
����OEF�ǵ���ֱ�������Σ�
��![]() OE2��
OE2��![]() ��
��
��OE��5.
��2����ͼ2������E���߶�BC��ʱ������P��PH��BC��H������E��EG��AC�ڵ�G��
�ߡ�ACB��45����PH��BC��
���HPC����PCH��45����
��PH��HC��
��PB2��PH2+BH2��
��4��26��PH2+��PH��8��2��
��PH��10��PH����2����ȥ����
��PH��CH��10��
��HB��2��PC��![]() =10
=10![]() ��
��
��EC��2��EG��AC����ACB��45����
��GC��GE=![]() ��
��
��PG��PC-GC=9![]() ��
��
�ߡ�FPE��45������HPC��
���FPH����EPG���ҡ�PHF����PGE��
���PFH�ס�PEG��
��![]() ��
��
��![]() ��
��
��HF��![]() ��
��
��BF��HB+HF=2+![]() ��
��![]() ��
��
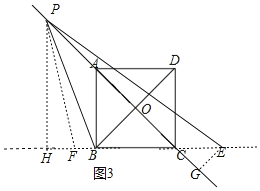
����E��BC�ӳ�����ʱ������P��PH��BC��H������E��EG��AC�ڵ�G��
ͬ���ɵã�PH��10��EG��CG��![]() ��PC=10
��PC=10![]() ����PFH�ס�PEG��
����PFH�ס�PEG��
��![]() ��PG=PC+GC=10
��PG=PC+GC=10![]() +
+![]() =11
=11![]() ��
��
��![]() ��
��
��FH��![]() ��
��
��BF��BH-FH=2��![]() ��
��![]() ��
��
����������BF�ij���![]() ��
��![]() ��
��
�ʴ�Ϊ��![]() ��
��![]()

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��������������Ƶ�����г��Ϸ������ֳ���������ijҽҩ��˾ÿ�¹̶������ס��������ͺŵķ��������ֹ�20��ֻ�������в�Ʒ����ȫ���۳���ԭ�ϳɱ������۵��ۼ�����������������
| �� | �� |
ԭ�ϳɱ� | 12 | 8 |
���۵��� | 18 | 12 |
������� | 1 | 0.8 |
��1�����ù�˾���·ݵ���������Ϊ300��Ԫ����ס��������ͺŵIJ�Ʒ�ֱ��Ƕ�����ֻ��
��2����˾ʵ�мƼ������ƣ�������ÿ����һֻ���ֻ��һ��������ɣ������˾���·�Ͷ���ܳɱ���ԭ���ܳɱ�+��������ܶ���������239��Ԫ��Ӧ�������żס��������ͺŵIJ�������ʹ���¹�˾���������������������������=�������멁Ͷ���ܳɱ���