题目内容
【题目】已知在以点O为圆心的两个同心圆中，大圆的弦AB交小圆于点C，D（如图）．
（1）求证：AC=BD；
（2）若大圆的半径R=10，小圆的半径r=8，且圆O到直线AB的距离为6，求AC的长．
【答案】（1）证明见解析；（2）8﹣
．
【解析】
试题（1）过O作OE⊥AB，根据垂径定理得到AE=BE，CE=DE，从而得到AC=BD；
（2）由（1）可知，OE⊥AB且OE⊥CD，连接OC，OA，再根据勾股定理求出CE及AE的长，根据AC=AE﹣CE即可得出结论．
试题解析：解：（1）证明：如答图，过点O作OE⊥AB于点E，
∵AE=BE，CE=DE，
∴BE﹣DE=AE﹣CE，即AC=BD.
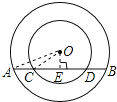
（2）由（1）可知，OE⊥AB且OE⊥CD，连接OC，OA，
∵OA=10，OC=8，OE=6，
∴
.
∴AC=AE﹣CE=8﹣．
练习册系列答案
相关题目
【题目】某市为支援灾区建设，计划向
、
两受灾地运送急需物资分别为60吨和140吨，该市甲、乙两地有急需物资分别为120吨和80吨，已知甲、乙两地运到、两地的每吨物资的运费如表所示：
甲 | 乙 | |
| 20元/吨 | 15元/吨 |
| 25元/吨 | 24元/吨 |
（1）设甲地运到地的急需物资为
吨，求总运费
（元）关于（吨）的函数关系式，并写出的取值范围；
（2）求最低总运费，并说明总运费最低时的运送方案．
