题目内容
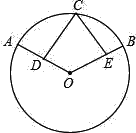
【题目】如图1,在等腰直角三角形![]() 中,
中,![]() ,点
,点![]() 在
在![]() 边上,连接
边上,连接![]() ,连接
,连接![]()
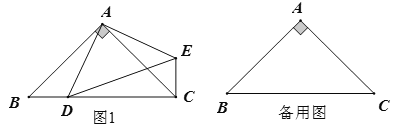
(1)求证:![]()
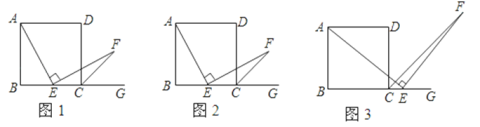
(2)点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,连接
,连接![]()
①补全图形并证明![]()
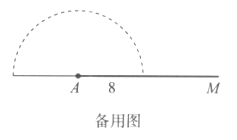
②利用备用图进行画图、试验、探究,找出当![]() 三点恰好共线时点
三点恰好共线时点![]() 的位置,请直接写出此时
的位置,请直接写出此时![]() 的度数,并画出相应的图形
的度数,并画出相应的图形
【答案】(1)证明见解析;(2)①见解析;②画图见解析,![]() .
.
【解析】
(1)先根据同角的余角相等推出∠BAD=∠CAE,再根据SAS证得△BAD≌△CAE,进而可得结论;
(2)①根据题意作图即可补全图形;利用轴对称的性质可得ME=AE,CM=CA,然后根据SSS可推出△CME≌△CAE,再利用全等三角形的性质和(1)题的∠BAD=∠CAE即可证得结论;
②当![]() 三点恰好共线时,设AC、DM交于点H,如图3,由前面两题的结论和等腰直角三角形的性质可求得∠DCM=135°,然后在△AEH和△DCH中利用三角形的内角和可得∠HAE=∠HDC,进而可得
三点恰好共线时,设AC、DM交于点H,如图3,由前面两题的结论和等腰直角三角形的性质可求得∠DCM=135°,然后在△AEH和△DCH中利用三角形的内角和可得∠HAE=∠HDC,进而可得![]() ,接着在△CDM中利用三角形的内角和定理求出∠CMD的度数,再利用①的结论即得答案.
,接着在△CDM中利用三角形的内角和定理求出∠CMD的度数,再利用①的结论即得答案.
解:(1)证明:∵AE⊥AD,∴∠DAE=90°,∴∠CAE+∠DAC=90°,
∵∠BAC=90°,∴∠BAD+∠DAC=90°,
∴∠BAD=∠CAE,
又∵BA=CA,DA=EA,
∴△BAD≌△CAE(SAS),
∴![]() ;
;
(2)①补全图形如图2所示,∵点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,∴ME=AE,CM=CA,
,∴ME=AE,CM=CA,
∵CE=CE,∴△CME≌△CAE(SSS),
∴![]() ,
,
∵∠BAD=∠CAE,
∴![]() ;
;
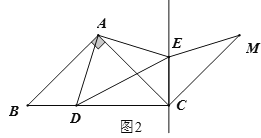
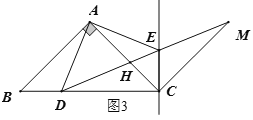
②当![]() 三点恰好共线时,设AC、DM交于点H,如图3,由(1)题知:
三点恰好共线时,设AC、DM交于点H,如图3,由(1)题知:![]() ,
,
∵△CME≌△CAE,∴![]() ,∴∠DCM=135°,
,∴∠DCM=135°,
在△AEH和△DCH中,∵∠AEH=∠ACD=45°,∠AHE=∠DHC,∴∠HAE=∠HDC,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目