��Ŀ����
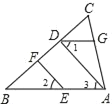
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���AOB��ֱ�������Σ���AOB=90������AB��y�ύ�ڵ�C.

��1������A=��AOC����˵������B=��BOC��
��2���ӳ�AB��x���ڵ�E����O��OD��AB������DOB=��EOB����A=��E������A�Ķ�����
��3����ͼ��OFƽ����AOM����BCO��ƽ���߽�FO���ӳ����ڵ�P����A=40��������ABO��O����תʱ����AB��y��������ʼ���ཻ�ڵ�C��������P�Ķ����Ƿ����ı䣿�����䣬������������ı䣬��˵������.
���𰸡�����������2��30����3����P�Ķ�������,��P=25�������ɼ�����
�����������š���AOB��ֱ��������
���A����B=90��,��AOC����BOC=90��
�ߡ�A=��AOC ���B=��BOC
�ơߡ�A����ABO=90��,��DOB����ABO=90��
���A=��DOB ����DOB=��EOB=��OAE=��OEA
�ߡ�DOB����EOB����OEA=90�� ���A=30��
�ǡ�P�Ķ�������,��P=25��.
�ߡ�AOM=90��-��AOC,��BCO=��A����AOC
��OFƽ����AOM,CPƽ����BCO
���FOM=45��-![]() ��AOC,��PCO=
��AOC,��PCO=![]() ��A��
��A��![]() ��AOC
��AOC
���P=180��-(��PCO����FOM��90��)=45��-![]() ��A=25��
��A=25��
��1����ֱ������������ǻ��༰�Ƚǵ������ȼ���֤����
��2����ֱ������������ǻ��ࡢ�������������DOB=��EOB=��OAE=��E��Ȼ�������Ƕ���֪��DOB+��EOB+��OEA=90�����Ӷ������DOB=30��������A=30����
��3���ɽ�ƽ���ߵ�����֪��FOM=45��- ![]() ��AOC ������PCO=
��AOC ������PCO= ![]() ��A+
��A+ ![]() ��AOC ���������٢������PCO+��FOM=45��+
��AOC ���������٢������PCO+��FOM=45��+ ![]() ��A���������������ڽǺͶ��������ת�����P�Ķ�����
��A���������������ڽǺͶ��������ת�����P�Ķ�����

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ��ij��̨����������ֺ���������֯20������װʳƷ��ҩƷ��������Ʒ���־������ʹ�100�ֵ������õ㣮���ƻ�20��������Ҫװ�ˣ�ÿ������ֻ��װ��ͬ�������ұ���װ�������ݱ����ṩ����Ϣ������������⣺
�������� | ʳƷ | ҩƷ | ������Ʒ |
ÿ���������������֣� | 6 | 5 | 4 |
ÿ�������˷ѣ�Ԫ/�֣� | 120 | 160 | 100 |
��1����װʳƷ�ij�����5����װҩƷ�ij���Ϊ__________����
��2����װʳƷ�ij���Ϊx����װҩƷ�ij���Ϊy������y��x�ĺ�����ϵʽ��
��3�����װʳƷ�ij���������7����װҩƷ�ij���������4������ô�����İ����м��ַ�������д��ÿ�ַ�����������ٷ��ã�
����Ŀ�������ҹ����õĸ��ٷ�չ�������������������֮�ƵĹ���Ҳ�õ�Ѹ�ٵķ�չ���±��ǽ�����ָ֤��ijһ������һ��������ı仯�������ע������������ʱ��ָ֤��Ϊ2019�㣬ÿһ������ʱָ����ǰһ����ȣ��Ǽ�Ϊ��![]() ��������Ϊ��
����������![]() ��
�� ![]()
���� | һ | �� | �� | �� | �� |
ָ���ı仯����ǰһ��Ƚϣ� |
|
|
|
|
|
��1���������ڶ�����ʱ����ָ֤���� �㣻
��2����������������ʱ����ָ֤������������������ʱ����ָ֤����ȣ��������˻��Ǽ�����?
��3��������һ������ʱ����ָ֤����ߣ���һ������ʱ����ָ֤����ͣ�