Question

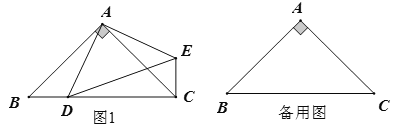
【题目】如图，△ABD，△AEC 都是等边三角形

（1）求证：BE＝DC .

（2）设 BE、DC 交于 M，连 AM，求的值.

Answer 1

【答案】（1）见解析 （2）1

【解析】

（1）利用△ABD、△AEC都是等边三角形，求证△DAC≌△BAE，然后即可得出BE=DC；
（2）在DM上截取DG=MB，连接AG，AM，易证△CAD≌△EAB，可得∠ADC=∠ABE，∠AEB=∠ACD，即可证明△ADG≌△ABM，可得∠DAG=∠BAM，AG=AM，即可判定△MAG为等边三角形，易得∠CAG=∠EAM，即可证明△CAG≌△EAM，可得CG=ME，即可解题．

（1）∵△ABD、△AEC都是等边三角形，
∴AD=AB，AE=AC，∠DAB=∠CAE=60°，
∴∠DAC=∠BAC+60°，
∠BAE=∠BAC+60°，
∴∠DAC=∠BAE，
在△DAC和△BAE中，

，
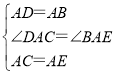∴△DAC≌△BAE（SAS），
∴BE=DC；
（2）在DM上截取DG=MB，连接AG，AM，

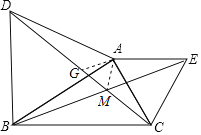
∵△ABD、△AEC等边三角形，
∴∠BAD=∠CAE=60°，AC=AE，AD=AB，
∴∠BAD+∠BAC=∠BAC+∠CAE，即∠BAE=∠CAD，
在△CAD和△EAB中，

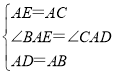
∴△CAD≌△EAB（SAS），
∴∠ADC=∠ABE，∠AEB=∠ACD，
在△ADG和△ABM中，

，
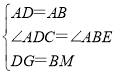∴△ADG≌△ABM（SAS），
∴∠DAG=∠BAM，AG=AM，
∵∠DAG+∠BAG=60°，
∴∠BAG+∠BAM=60°，即∠MAG=60°，
∴△MAG为等边三角形，∠MAG+∠CAM=∠CAM+∠CAE，即∠CAG=∠EAM，
∴MA=MG，
在△CAG和△EAM中，

，
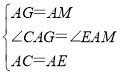∴△CAG≌△EAM（SAS），
∴CG=ME，
∴MD+ME=DG+MG+MC+MG=MB+MC+2MA，
∴=1．