题目内容
【题目】平面直角坐标系中,直线l1:y=﹣ ![]() x+3与x轴交于点A,与y轴交于点B,直线l2:y=kx+2k与x轴交于点C,与直线l1交于点P.
x+3与x轴交于点A,与y轴交于点B,直线l2:y=kx+2k与x轴交于点C,与直线l1交于点P.
(1)当k=1时,求点P的坐标;
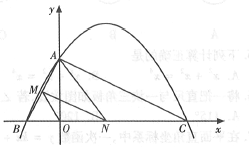
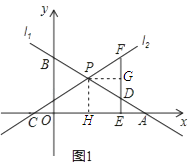
(2)如图1,点D为PA的中点,过点D作DE⊥x轴于E,交直线l2于点F,若DF=2DE,求k的值;
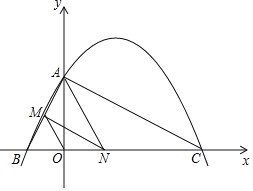
(3)如图2,点P在第二象限内,PM⊥x轴于M,以PM为边向左作正方形PMNQ,NQ的延长线交直线l1于点R,若PR=PC,求点P的坐标.
【答案】
(1)解:当k=1时,直线l2为y=x+2.
解方程组 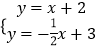 ,
,
解得 ![]() ,
,
∴P( ![]() ,
, ![]() );
);
(2)解:当y=0时,kx+2k=0,
∵k≠0,
∴x=﹣2,
∴C(﹣2,0)则OC=2,
当y=0时,﹣ ![]() x+3=0,
x+3=0,
∴x=6,
∴A(6,0),OA=6,
过点P作PG⊥DF于点G,
在△PDG和△ADE中,
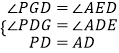 ,
,
∴△PDG≌△ADE,
得DE=DG= ![]() DF,
DF,
∴PD=PF,
∴∠PFD=∠PDF
∵∠PFD+∠PCA=90°,∠PDF+∠PAC=90°
∴∠PCA=∠PAC,
∴PC=PA
过点P作PH⊥CA于点H,
∴CH= ![]() CA=4,
CA=4,
∴OH=2,
当x=2时,y=﹣ ![]() ×2+3=2代入y=kx+2k,得k=
×2+3=2代入y=kx+2k,得k= ![]()
(3)解:直角△PQR和直角△PMC中,
![]() ,
,
∴Rt△PMC≌Rt△PQR,
∴CM=RQ,
∴NR=NC,
设NR=NC=a,则R(﹣a﹣2,a),
代入y=﹣ ![]() x+3,
x+3,
得﹣ ![]() (﹣a﹣2)+3=a,解得a=8,
(﹣a﹣2)+3=a,解得a=8,
设P(m,n),则 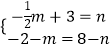 ,
,
解得 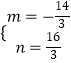 ,
,
∴P(﹣ ![]() ,
, ![]() ).
).
【解析】(1)解两个函数解析式组成的方程组即可求解;(2)过点P作PG⊥DF于点G,易证△PDG≌△ADE,点P作PH⊥CA于点H,可以证明H是AC的中点,则H的坐标即可求得,进而求得P的坐标,进而求得k的值;(3)Rt△PMC≌Rt△PQR,则RQ=MC,设NR=NC=a,则R(﹣a﹣2,a),代入y=﹣ ![]() x+3,求得a的值,设P(m,n),根据P在直线l1上和RQ=MC即可列方程组求解.
x+3,求得a的值,设P(m,n),根据P在直线l1上和RQ=MC即可列方程组求解.

 名校课堂系列答案
名校课堂系列答案