题目内容
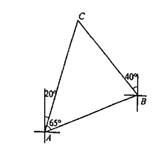
【题目】如图,-艘船由A港沿北偏东65°方向航行![]() km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向,求A,C两港之间的距离.
km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向,求A,C两港之间的距离.
【答案】![]() .
.
【解析】
过点B作BM⊥AC,垂足为M,由已知可得:∠BAM=45°,继而可求得AM、BM的长,在Rt△CBM中,利用三角函数可求得CM=BM·tan30°=10![]() ,继而根据AC=AM+CM即可求得答案.
,继而根据AC=AM+CM即可求得答案.
过点B作BM⊥AC,垂足为M,
由已知可得:∠BAM=∠BAE-∠CAE=65°-20°=45°,
∴AM=AB·cos45°=30![]() =30,BM=AM=30;
=30,BM=AM=30;
在Rt△CBM中,∠CBM=∠GBH+∠HBA-∠CBG-∠ABM
=90°+25°-40°-45°=30°,
∴CM=BM·tan30°=30×![]() =10
=10![]() ,
,
∴AC=AM+CM=30+10![]() ,
,
答:A,C两港之间的距离为(![]() )千米.
)千米.


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目