题目内容
【题目】如图,![]() 中,
中,![]() 分别是
分别是![]() 的中点.
的中点.

![]() 求证:四边形
求证:四边形![]() 是菱形
是菱形
![]() 如果
如果![]() ,求四边形
,求四边形![]() 的面积.
的面积.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)由平行四边形的性质可得BC=AD,BC∥AD,由中点的性质可得EC=AF,可证四边形AECF为平行四边形,由直角三角形的性质可得AE=EC,即可得结论;
(2)由勾股定理可求AC的长,可求S△ABC=![]() AB×AC=2
AB×AC=2![]() ,即可求四边形AECF的面积.
,即可求四边形AECF的面积.
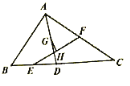
证明:(1)∵在ABCD中,
∴BC=AD,BC∥AD,
又∵E,F分别是边BC,AD的中点,
∴EC=![]() BC,AF=
BC,AF=![]() AD,
AD,
∴EC=AF,且EC∥AF,
∴四边形AECF为平行四边形.
在Rt△ABC中,∠BAC=90°,E是BC边中点,
∴AE=EC,
∴四边形AECF是菱形;
(2)∵∠BAC=90°,AB=2,BC=4,
∴AC=![]() =2
=2![]() ,
,
∴S△ABC=![]() AB×AC=2
AB×AC=2![]() ,
,
∵点E是BC的中点,
∴S△AEC=![]() S△ABC=
S△ABC=![]() ,
,
∵四边形AECF是菱形
∴四边形AECF的面积=2S△AEC=2![]() .
.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
【题目】某天,一蔬菜经营户用180元钱从蔬菜批发市场批了西红柿和豆角共40千克到菜市场去卖,西红柿和豆角这天的批发价与零售价如下表所示:
品名 | 西红柿 | 豆角 |
批发价(单位:元/千克) | 3.6 | 4.6 |
零售价(单位:元/千克) | 5.4 | 7.5 |
问:他当天卖完这些西红柿和豆角能赚多少钱?