Question

【题目】如图，AC平分∠BCD，AB=AD, AE⊥BC于E,AF⊥CD于F

（1）若∠ABE= 50° ，求∠CDA的度数.

（2）若AE=4，BE=2，CD=6，求四边形AECD 的面积.

Answer 1

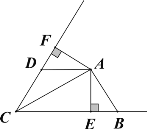
【答案】（1）130° （2）28

【解析】

（1）由角平分线的性质定理证得AE=AF，进而证出△ABE≌△ADF，再得出∠CDA=130°；
（2）四边形AECD的面积化为△AEC的面积+△ACD的面积，根据三角形面积公式求出结论．

（1）∵AC平分∠BCD，AE⊥BC AF⊥CD，
∴AE=AF，
在Rt△ABE和Rt△ADF中，

∴Rt△ABE≌Rt△ADF，
∴∠ADF=∠ABE=50°，
∴∠CDA=180°-∠ADF=130°；
（2）由（1）知：Rt△ABE≌Rt△ADF，
∴FD=BE=2，AF=AE=4，CE=CF=CD+FD=8，
∴四边形AECD的面积=△AEC的面积+△ACD的面积=CEAE+CDAF=×4×8+×4×6=28．