题目内容
【题目】问题提出:
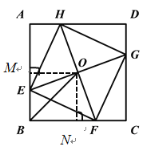
(1)如图①,若正方形![]() 的边长为6,点
的边长为6,点![]() 分别为边
分别为边![]() 上的点,且
上的点,且![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,则
,则![]() ;
;
问题探究:
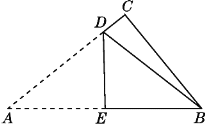
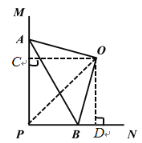
(2)如图②,![]() ,
,![]() 是等腰直角三角形,顶点
是等腰直角三角形,顶点![]() 分别在
分别在![]() 的两边上,试说明点
的两边上,试说明点![]() 在
在![]() 的平分线上;
的平分线上;
问题解决:
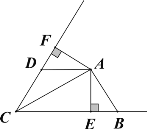
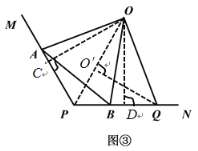
(3)如图③,![]() ,
,![]() 是等边三角形,顶点
是等边三角形,顶点![]() 分别在
分别在![]() 的两边上,点
的两边上,点![]() 在
在![]() 上,且
上,且![]() ,连接
,连接![]() ,求
,求![]() 的最小值.
的最小值.

【答案】(1)3![]() ;(2)见解析;(3)3
;(2)见解析;(3)3![]() .
.
【解析】
(1)先证明△AEH≌△BFE≌△CGF≌△DHG,可得出四边形GHEF是菱形,再根据全等三角形角之间的关系,又可得出菱形的一个角是直角,那么就可得出四边形GHEF是正方形.过点O分别作OM⊥AB于点M,ON⊥BC于点N,根据AAS易得△EOM≌△FON,得出OC=OD,根据角平分线的判定定理可得OB平分∠ABC,根据BO=![]() BD可得出结果..
BD可得出结果..
(2)过点O分别作OC⊥AP于点C,OD⊥PN于点D,证明△EOC≌△BOD,得出OC=OD,根据角平分线的判定定理可得出结果.
(3)过点O分别作OC⊥AP于点C,OD⊥PN于点D,同(2)中证法可得点O在∠MPN的平分线上,连接PO,过点Q作QO′⊥PO于点O′,则QO′即为QO的最小值,在Rt△PQO′中求出QO′的值即可.
解:(1)∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA,
∵HA=EB=FC=GD,
∴AE=BF=CG=DH,
∴△AEH≌△BFE≌△CGF≌△DHG,
∴EF=FG=GH=HE,
∴四边形EFGH是菱形,
∵△DHG≌△AEH,
∴∠DHG=∠AEH,
∵∠AEH+∠AHE=90°,
∴∠DHG+∠AHE=90°,
∴∠GHE=90°,
∴四边形EFGH是正方形.
∴EO=FO,∠EOF=90°.
过点O分别作OM⊥AB于点M,ON⊥BC于点N,
根据AAS易得△EOM≌△FON,
∴MO=NO,
∴BO平分∠ABC,
∴BO=![]() BD=
BD=![]() BC=3
BC=3![]() .
.
图①
(2)过点O分别作OC⊥AP于点C,OD⊥PN于点D,
∵∠APB=90°,
∴∠AOB=∠COD=90°,
∴∠AOC=∠BOD,
又AO=BO,∠ACO=∠ODB,
∴△AOC≌△BOD(AAS),
∴CO=DO,
又OC⊥PM,OD⊥PN,
∴点![]() 在
在![]() 的平分线上.
的平分线上.
(3) 过点O分别作OC⊥PM于点C,OD⊥PN于点D,同(2)中证法可得点O在∠MPN的平分线上,连接PO,过点Q作QO′⊥PO于点O′
∵OP为∠MPN的平分线,
∴∠OPN=60°,
又PQ=6,∴PO′=3,
∴QO′=3![]() .
.
即QO的最小值为3![]() .
.

 阅读快车系列答案
阅读快车系列答案