题目内容
【题目】四边形ABCD是正方形,AC是对角线,E是平面内一点,且![]() ,过点C作
,过点C作![]() ,且
,且![]() 。连接AE、AF,M是AF的中点,作射线DM交AE于点N.
。连接AE、AF,M是AF的中点,作射线DM交AE于点N.
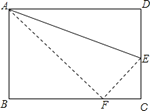
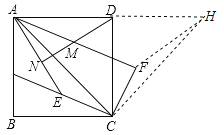
(1)如图1,若点E,F分别在BC,CD边上。
求证:①![]() ;
;
②![]() ;
;
(2)如图2,若点E在四边形ABCD内,点F在直线BC的上方,求![]() 与
与![]() 的和的度数。
的和的度数。

【答案】(1)①见解析;②见解析;(2)![]()
【解析】
(1)根据已知及正方形的性质,全等三角形的判定,全等三角形的性质的计算,可知①∠BAE=∠DAF是否成立;可知②DN⊥AE是否成立;
(2)根据已知及正方形的性质,全等三角形的判定,全等三角形的性质的计算,求出∠EAC与∠ADN的和的度数.
(1)证明:①在正方形ABCD中,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
②∵M是AF的中点,
∴![]() ,
,
由①可知![]() .
.
∵![]() .
.
∵![]()
∴![]()
∴![]()
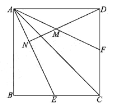
(2)解:延长AD至H,使得![]() ,连结FH,CH.
,连结FH,CH.
∵![]() ,
,
∴![]() .
.
在正方形ABCD屮,AC是对角线,
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴![]()
又∵![]() ,
,
∴![]()
∵M是AF的中点,D是AH的中点,
∴![]() .
.
∴![]()
∴![]()

练习册系列答案
相关题目
【题目】如图是用长度相等的小棒按一定规律摆成的一组图案
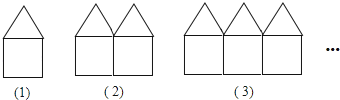
(1)填写下表:
图形序号 | ① | ② | ③ | …… | ⑧ |
每个图案中小棒的数量 | 6 | 11 | …… |
(2)请填写出第![]() 个图案中小棒的数量(用含
个图案中小棒的数量(用含![]() 的代数式表示);
的代数式表示);
(3)第30个图案中小棒有多少根?