Question

【题目】如图所示，折叠矩形ABCD的一边AD，使点D落在BC边上的点F处，已知AB=8，BC=10，

（1）求BF的长；

（2）求△ECF的面积．

Answer 1

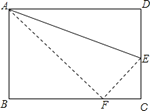
【答案】（1）BF=6；（2）6.

【解析】

（1）因为点F为点D的折后的落点，所以△AFE≌△ADE，由此可得AF=AD=10cm，在△ABF中利用勾股定理，可得BF的值，
（2）先求出DE的长，进而求出CE的长，利用三角形的面积公式即可求出△ECF的面积．

（1）∵△ADE折叠后的图形是△AFE，

∴△AFE≌△ADE

∴AD=AF，∠D=∠AFE，DE=EF，

∵AD=BC=10，

∴AF=AD=10，

又∵AB=8，在Rt△ABF中，根据勾股定理，得AB2+BF2=AF2，

∴82+BF2=102，

∴BF=6；

故答案为：6.

（2）则可得FC=BC-BF=10-6=4，

设EC的长为x，

∴DE=（8-x），

∵FC=4，

在Rt△EFC中，根据勾股定理，得：FC2+EC2=EF2，

∴42+x2=（8-x）2，

即16+x2=64-16x+x2，

化简，得16x=48，

∴x=3，

故EC=3.

∴.

故答案为：6.