题目内容
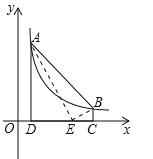
【题目】如图,一次函数y=﹣![]() x+2分别交y轴、x轴于A,B两点,抛物线y=﹣x2+bx+c过A,B两点.
x+2分别交y轴、x轴于A,B两点,抛物线y=﹣x2+bx+c过A,B两点.
(1)求这个抛物线的解析式;
(2)作垂直于x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t取何值时,△NAB的面积有最大值?最大值是多少?
(3)在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.

【答案】(1) y=﹣x2+![]() x+2 (2)4 (3)(0,6),(0,﹣2)或(4,4)
x+2 (2)4 (3)(0,6),(0,﹣2)或(4,4)
【解析】试题分析:(1)首先求得A、B点的坐标,然后利用待定系数法求抛物线的解析式;
(2)本问要点是求得线段MN的表达式,这个表达式是关于t的二次函数,利用二次函数的极值求线段MN的最大值;
(3)本问要点是明确D点的可能位置有三种情形,如答图2所示,不要遗漏.其中D1、D2在y轴上,利用线段数量关系容易求得坐标;D3点在第一象限,是直线D1N和D2M的交点,利用直线解析式求得交点坐标.
试题解析:(1)∵y=﹣![]() +2分别交y轴、x轴于A、B两点,
+2分别交y轴、x轴于A、B两点,
∴A、B点的坐标为:A(0,2),B(4,0),
将x=0,y=2代入y=﹣x2+bx+c得c=2,
将x=4,y=0代入y=﹣x2+bx+c得0=﹣16+4b+2,解得b=![]() ,
,
∴抛物线解析式为:y=﹣x2+![]() x+2;
x+2;
(2)如图1,设MN交x轴于点E,
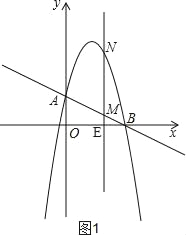
则E(t,0),BE=4﹣t.
∵tan∠ABO=![]() =
=![]() ,
,
∴ME=BEtan∠ABO=(4﹣t)×![]() =2﹣
=2﹣![]() t.
t.
又N点在抛物线上,且xN=t,∴yN=﹣t2+![]() t+2,
t+2,
∴MN=yN﹣ME=﹣t2+![]() t+2﹣(2﹣
t+2﹣(2﹣![]() t)=﹣t2+4t
t)=﹣t2+4t
∴当t=2时,MN有最大值4;
(3)由(2)可知,A(0,2),M(2,1),N(2,5).
以A、M、N、D为顶点作平行四边形,D点的可能位置有三种情形,
如图2所示.
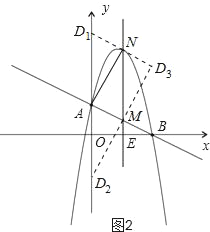
(i)当D在y轴上时,设D的坐标为(0,a)
由AD=MN,得|a﹣2|=4,解得a1=6,a2=﹣2
从而D为(0,6)或D(0,﹣2),
(ii)当D不在y轴上时,由图可知D3为D1N与D2M的交点,
易得D1N的方程为y=﹣![]() x+6,D2M的方程为y=
x+6,D2M的方程为y=![]() x﹣2,
x﹣2,
由两方程联立解得D为(4,4)
故所求的D点坐标为(0,6),(0,﹣2)或(4,4).

【题目】东莞市出租车收费标准如下表所示,根据此收费标准,解决下列问题:
行驶路程 | 收费标准 |
不超出 | 起步价8元 |
超出 | 2.6元/ |
(1)若行驶路程为![]() ,则打车费用为______元;
,则打车费用为______元;
(2)若行驶路程为![]() ,则打车费用为______元(用含
,则打车费用为______元(用含![]() 的代数式表示);
的代数式表示);
(3)某同学周末放学回家,已知打车费用为34元,则他家离学校多少千米?