��Ŀ����
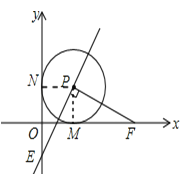
����Ŀ����֪��ƽ��ֱ������ϵxOy�У�O������ԭ�㣬��P��1��1��ΪԲ�ĵ���P��x�ᡢy��ֱ������ڵ�M�͵�N����F�ӵ�M��������x����������ÿ��1����λ���ȵ��ٶ��˶�������PF������P��PE��PF��y���ڵ�E�����F�˶���ʱ����t�루t��0��
��1������E��y��ĸ������ϣ���ͼ��ʾ������֤��PE=PF��
��2���ڵ�F�˶������У���OE=a��OF=b�����ú�a�Ĵ���ʽ��ʾb��
��3������F���ڵ�M�ĶԳƵ�F��������M��E��F������������ߵĶԳ��ύx���ڵ�Q������QE���ڵ�F�˶������У��Ƿ����ijһʱ�̣�ʹ���Ե�Q��O��EΪ��������������Ե�P��M��FΪ��������������ƣ������ڣ���ֱ��д��t��ֵ���������ڣ���˵�����ɣ�

���𰸡�(1)��֤�����̼�������(2)��b=2+a��b=2��a��(3)��t=![]() ��t=
��t=![]() ��t=2��
��t=2��![]()
�����������������(1)������PM��PN���������ߵ����ʵó�PM=PN�����ݾ�NPM=��EPF=90���ó���NPE=��MPF���Ӷ�˵����PMF����PNEȫ�ȣ��Ӷ�˵��PE=PF��(2)������t��1��1��t��1����������a��b�Ĺ�ϵ��(3)���������������εļ��ֲ�ͬ��������t��ֵ.
���������(1)����ͼ������PM��PN��
�ߡ�P��x�ᣬy��ֱ������ڵ�M�͵�N�� ��PM��MF��PN��ON��PM=PN��
���PMF=��PNE=90������NPM=90������PE��PF�� ��NPE=��MPF=90�㩁��MPE��
����PMF����PNE�У���NPE=��MPF PN=PM ��PNE=��PMF �����PMF�ա�PNE��ASA�� ��PE=PF��
(2)���⣺����t��1ʱ����E��y��ĸ������ϣ�
�ɣ�1������PMF�ա�PNE����NE=MF=t��PM=PN=1�� ��b=OF=OM+MF=1+t��a=NE��ON=t��1��
��b��a=1+t����t��1��=2����b=2+a��
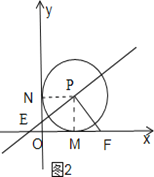
��0��t��1ʱ����ͼ2����E��y����������ԭ���ϣ�
ͬ����֤��PMF�ա�PNE�� ��b=OF=OM+MF=1+t��a=ON��NE=1��t�� ��b+a=1+t+1��t=2�� ��b=2��a��
(3)��t=![]() ��t=
��t=![]() ��t=2��
��t=2��![]()