题目内容
【题目】(1)解不等式5x+2≥3(x﹣1),并把它的解集在数轴上表示出来.
![]()
(2)写出一个实数k,使得不等式x<k和(1)中的不等式组成的不等式组恰有3个整数解.
【答案】(1)x≥﹣2.5,数轴见解析;(2)1
【解析】
(1)先去括号,再移项得到5x﹣3x≥﹣3﹣2,然后合并后系数化为1即可,再用数轴表示解集即可求解.
(2)根据题意可得0<k≤1满足条件,依此写出即可求解.
解:(1)5x+2≥3(x﹣1),
去括号得5x+2≥3x﹣3,
移项得5x﹣3x≥﹣3﹣2,
合并得2x≥﹣5,
系数化为1得x≥﹣2.5,
用数轴表示为:
![]()
(2)∵一个实数k,使得不等式x<k和(1)中的不等式组成的不等式组恰有3个整数解,
∴0<k≤1,
∴故k=1满足条件.

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案【题目】某中学开展普通话演讲比赛,九(1)、(2)两个班根据初赛成绩各选出5名选手参加复赛,10名选手的复赛成绩如图所示:
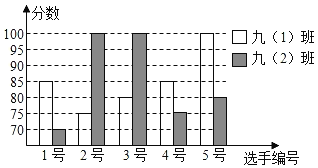
(1)根据如图补充完成下面的成绩统计分析表:
平均数 | 中位数 | 众数 | 方差 | 合格率 | 优秀率 | |
九(1)班 | 85 |
| 85 |
|
| 60% |
九(2)班 | 85 | 80 |
| 160 | 100% |
|
(2)九(1)班学生说他们的复赛成绩好于九(2)班,结合图表,请你给出三条支持九(1)班学生观点的理由.
(3)如果从复赛成绩100分的3名选手中任选2人参加学校决赛,求选中的两位选手恰好一位来自于九(1)班,另一位来自于九(2)班的概率.
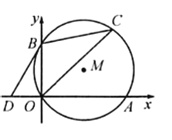
【题目】如图,![]() 是以O为圆心,AB长为直径的半圆弧,点C是AB上一定点.点P是
是以O为圆心,AB长为直径的半圆弧,点C是AB上一定点.点P是![]() 上一动点,连接PA,PC,过点P作PD⊥AB于D.已知AB=6cm,设A、P两点间的距离为x cm,P、C两点间的距离为y1 cm,P、D两点间的距离为y2 cm.
上一动点,连接PA,PC,过点P作PD⊥AB于D.已知AB=6cm,设A、P两点间的距离为x cm,P、C两点间的距离为y1 cm,P、D两点间的距离为y2 cm.
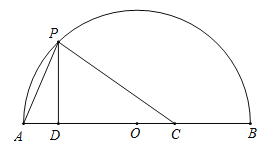
小刚根据学习函数的经验,分别对函数y1和y2随自变量x变化而变化的规律进行了探究.下面是小刚的探究过程,请将它补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到y1和y2与x的几组对应值:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 4.00 | 3.96 | m | 3.61 | 3.27 | 2.77 | 2.00 |
y2/cm | 0.00 | 0.99 | 1.89 | 2.60 | 2.98 | 2.77 | 0.00 |
经测量,m的值是 ;(保留一位小数)
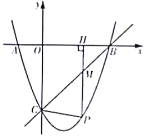
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),点(x,y2),并画出函数y1, y2的图象;

(3)结合函数图象,回答问题:△APC为等腰三角形时,AP的长度约为 cm.
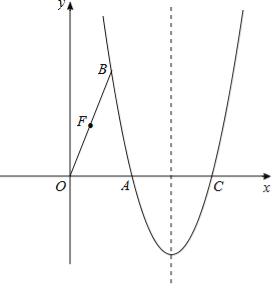
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 50 | 60 | 70 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),则当售价x定为多少元时,厂商每天能获得最大利润?最大利润是多少?
(3)如果超市要获得每天不低于1350元的利润,且符合超市自己的规定,那么该商品每千克售价的取值范围是多少?请说明理由.