题目内容
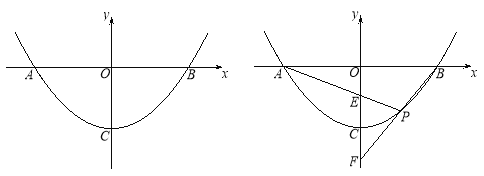
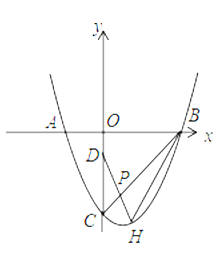
【题目】如图,在平面直角坐标系中,抛物线与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,且
,且![]() .
.
(1)求抛物线的解析式;
(2)已知点![]() ,点
,点![]() 为线段
为线段![]() 上一动点,延长
上一动点,延长![]() 交抛物线于点
交抛物线于点![]() ,连结
,连结![]() .
.
①当四边形![]() 面积为9,求点
面积为9,求点![]() 的坐标;
的坐标;
②设![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(1)y=![]() x2﹣x﹣4;(2)①点H的坐标为(2,﹣4)或(
x2﹣x﹣4;(2)①点H的坐标为(2,﹣4)或(![]() ,﹣
,﹣![]() );②m的最大值为
);②m的最大值为![]() .
.
【解析】
(1)根据题意可设设抛物线的解析式为y=a(x+2)(x﹣4),易得C(0,﹣4),利用待定系数法确定函数关系式即可;
(2)①过点H作HM⊥x轴与点M,交BC于点N,设H(h,![]() h2﹣h﹣4),根据S=S梯形ODHM+S△BHM得到关于h的方程,然后求解方程即可;
h2﹣h﹣4),根据S=S梯形ODHM+S△BHM得到关于h的方程,然后求解方程即可;
②设BC的解析式为y=kx+b,将B、C坐标代入求得BC的解析式为y=x﹣4,设H(n,![]() n2﹣n﹣4),N(n,n﹣4),易证△PHN∽△PCD,利用相似三角形的性质与配方法即可得到m的最大值.
n2﹣n﹣4),N(n,n﹣4),易证△PHN∽△PCD,利用相似三角形的性质与配方法即可得到m的最大值.
(1)设抛物线的解析式为y=a(x+2)(x﹣4),
∵B(4,0),OB=OC,
∴C(0,﹣4),
代入上式可得:a(0+2)(0﹣4)=﹣4,
解得a=![]() ,
,
∴y=![]() (x+2)(x﹣4)=
(x+2)(x﹣4)=![]() x2﹣x﹣4;
x2﹣x﹣4;
(2)①过点H作HM⊥x轴与点M,交BC于点N,
设H(h,![]() h2﹣h﹣4),
h2﹣h﹣4),
则S=S梯形ODHM+S△BHM=![]() (1﹣
(1﹣![]() h2+h+4)·h+
h2+h+4)·h+![]() (﹣
(﹣![]() h2+h+4)(4﹣h),
h2+h+4)(4﹣h),
整理得﹣h2+![]() h+8=9,
h+8=9,
解得h1=2,h2=![]() ,
,
∴点H的坐标为(2,﹣4)或(![]() ,﹣
,﹣![]() );
);
②设BC的解析式为y=kx+b,
将B(4,0),C(0,﹣4)代入函数解析式,得
![]() ,
,
解得k=1,b=﹣4,
∴BC的解析式为y=x﹣4,
设H(n,![]() n2﹣n﹣4),N(n,n﹣4),
n2﹣n﹣4),N(n,n﹣4),
∴HN= n﹣4﹣(![]() n2﹣n﹣4)=﹣
n2﹣n﹣4)=﹣![]() n2+2n,
n2+2n,
∵HN∥CD,
∴△PHN∽△PCD,
∴![]() =﹣
=﹣![]() n2+
n2+![]() n=﹣
n=﹣![]() (n﹣2)2+
(n﹣2)2+![]() ,
,
则当n=2时,m=![]() 有最大值
有最大值![]() .
.


【题目】某书店为了迎接“读书节”制定了活动计划,以下是活动计划书的部分信息:
“读书节”活动计划书 | ||
书本类别 | A类 | B类 |
进价(单位:元) | 18 | 12 |
备注 | 1.用不超过16800元购进A,B两类图书共1000本; 2.A类图书不少于600本; …… |
(1)陈经理查看计划数时发现:A类图书的标价是B类图书标价的1.5倍,若顾客用540元购买图书,能单独购买A类图书的数量恰好比单独购买B类图书的数量少10本,请求出A,B两类图书的标价;
(2)经市场调查后,陈经理发现他们高估了“读书节”对图书销售的影响,便调整了销售方案,A类图书每本标价降低a元(0<a<5)销售,B类图书价格不变,那么书店应如何进货才能获得最大利润?
【题目】光明中学全体学生900人参加社会实践活动,从中随机抽取50人的社会实践活动成绩制成如图所示的条形统计图,结合图中所给信息解答下列问题:
![]() 填写下表:
填写下表:
中位数 | 众数 | |
随机抽取的50人的社会实践活动成绩 |
![]() 估计光明中学全体学生社会实践活动成绩的总分.
估计光明中学全体学生社会实践活动成绩的总分.