��Ŀ����
ij�����P���˶���Q������ʱ��Ϊ7�룬���˶��ٶ�v����ÿ�룩����ʱ��t���룩�ĺ�����ϵ��ͼ��ʾ��ijѧϰС�龭��̽�����֣�������ǰ��3���˶���·������ֵ�ϵ��ھ���AODB�������������ѧ֪ʶ����֪��������ǰt��3��t��7�����˶���·������ֵ�ϵ��ھ���AODB�����������BDNM�����֮�ͣ�
����������Ϣ������������⣺
��1����3��t��7ʱ���ú�t��ʽ�ӱ�ʾv��
��2���ֱ����������0��t��3��3��t��7ʱ���˶���·��s���ף�����ʱ��t���룩�ĺ�����ϵʽ��
��3����������P���˶���Q��·�̵� ʱ���õ�ʱ�䣮
ʱ���õ�ʱ�䣮
��1��v=2t��4����2�� ����3��6.
����3��6.
���������������1����ֱ��BC�Ľ���ʽΪv=kt+b�����ô���ϵ�����Ϳ������t��v�Ĺ�ϵʽ����2����·��=�ٶȡ�ʱ�䣬�Ϳ��Ա�ʾ��������0��t��3��3��t��7ʱ���˶���·��s���ף�����ʱ��t���룩�ĺ�����ϵʽ����3����������ǰt��3��t��7�����˶���·������ֵ�ϵ��ھ���AODB�����������BDNM�����֮�������·�̣�Ȼ�� �������ʽ�Ϳ������tֵ��
�������ʽ�Ϳ������tֵ��
�����������1����ֱ��BC�Ľ���ʽΪv=kt+b�������⣬�� ����ã�
����ã� .
.
�൱3��n��7ʱ��v=2t��4.
��2�������⣬�� .
.
��3��P���˶���Q���·��Ϊ��2��3+��2+10������7��3���� =30.
=30.
��30�� =21.
=21.
�� ����ã�t1=��2����ȥ����t2=6.
����ã�t1=��2����ȥ����t2=6.
��������P���˶���Q����·�̵� ʱ���õ�ʱ��Ϊ6��.
ʱ���õ�ʱ��Ϊ6��.
���㣺1.һ�κ�����Ӧ�ã�2.����ϵ������Ӧ�ã�3.ֱ���ϵ�������뷽�̵Ĺ�ϵ��4.����˼������ν��˼���Ӧ��.

 ��У����ϵ�д�
��У����ϵ�д� ��
�� �Ƿ���������
�Ƿ��������� ͼ���ϵ�������.
ͼ���ϵ�������.
 ��ȡֵ��Χ.
��ȡֵ��Χ. ��
��

 ��
�� ����λ��Ԫ����������Ӫʱ��
����λ��Ԫ����������Ӫʱ�� ����λ���죩֮��ֱ������ϵʽ��
����λ���죩֮��ֱ������ϵʽ�� ��
�� ����ͼ��ʾ.
����ͼ��ʾ.
 = Ԫ,ÿ�����ĸ�װ��b= Ԫ.������Ӫ ��Ϳ��Դӽ�ʡȼ�Ϸ����ջظ�װ�ɱ�.
= Ԫ,ÿ�����ĸ�װ��b= Ԫ.������Ӫ ��Ϳ��Դӽ�ʡȼ�Ϸ����ջظ�װ�ɱ�.
 ʱ���õ�ʱ�䣮
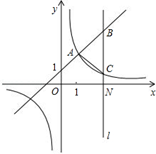
ʱ���õ�ʱ�䣮 ��m��0����ͼ���й�����A��1��2����ֱ��l��x���ڵ�N��3��0������һ�κ����ͷ�����������ͼ��ֱ��ڵ�B��C��
��m��0����ͼ���й�����A��1��2����ֱ��l��x���ڵ�N��3��0������һ�κ����ͷ�����������ͼ��ֱ��ڵ�B��C��