题目内容
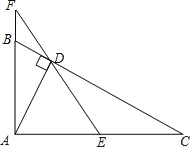
【题目】如图,已知∠BAC=90°,AD⊥BC于D,E是AC的中点,ED的延长线交AB的延长线于点F.求证:
(1)△DFB∽△AFD;
(2)AB:AC=DF:AF.
【答案】(1)详见解析;(2)详见解析.
【解析】试题分析:(1)由已知条件得到∠BAC=∠ADB=![]() ,根据余角的性质得到∠BAD=∠C,由直角三角形的性质和对顶角相等得到∠BAD=∠BDF,即可得到结论;
,根据余角的性质得到∠BAD=∠C,由直角三角形的性质和对顶角相等得到∠BAD=∠BDF,即可得到结论;
(2)根据已知条件推出△ABD∽△CAD;于是得到![]() 由于△DFB∽△AFD;于是得到
由于△DFB∽△AFD;于是得到![]()
等量代换即可得到结论.
试题解析:(1)∵∠BAC=![]() ,AD⊥BC于D,
,AD⊥BC于D,
∴∠BAC=∠ADB=![]() ,
,
∴∠BAD+∠ABD=∠ABD+∠C=![]() ,
,
∴∠BAD=∠C,
∵E是AC的中点,
∴DE=CE,
∴∠C=∠EDC,
∵∠EDC=∠BDF,
∴∠BAD=∠BDF,
∵∠F=∠F,
∴△DFB∽△AFD;
(2)∵AD⊥BC,
∴∠ADB=∠ADC=![]() ,
,
∴∠BAD+∠DAC=![]() ,∠DAC+∠ACD=
,∠DAC+∠ACD=![]() ,
,
∴∠BAD=∠ACD,
∵∠ADB=∠ADC,
∴△ABD∽△CAD;
∴![]()
∵△DFB∽△AFD;
∴![]()
∴AB:AC=DF:AF.

 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案【题目】在“节能减排,做环保小卫士”活动中,小明对两种照明灯的使用情况进行了调查,得出如表所示的数据:
功率 | 使用寿命 | 价格 | |
普通白炽灯 |
|
|
|
优质节能灯 |
|
|
|
已知这两种灯的照明效果一样,小明家所在地的电价是每度![]() 元.(注:用电度数
元.(注:用电度数![]() 功率(千瓦)
功率(千瓦)![]() 时间(小时),费用
时间(小时),费用![]() 灯的售价
灯的售价![]() 电费);如:若选用一盏普通白炽灯照明
电费);如:若选用一盏普通白炽灯照明![]() 小时,那么它的费用为
小时,那么它的费用为![]() (元),请解决以下问题:
(元),请解决以下问题:
(1)在白炽灯的使用寿命内,设照明时间为![]() 小时,请用含
小时,请用含![]() 的代数式分别表示用一盏白炽灯的费用
的代数式分别表示用一盏白炽灯的费用![]() ,(元)和一盏节能灯的费用
,(元)和一盏节能灯的费用![]() (元);
(元);
(2)在白炽灯的使用寿命内,照明多少小时时,使用这两种灯的费用相等?
(3)如果计划照明![]() 小时,购买哪一种灯更省钱?请你通过计算说明理由.
小时,购买哪一种灯更省钱?请你通过计算说明理由.