��Ŀ����
����Ŀ����֪����ͼ1����ƽ��ֱ������ϵ�У���A��B��C�����������ϣ���OA=OB=OC����ABC�����Ϊ9����P��C�������y�Ḻ������1����λ/����ٶ������˶�������PA��PB��D����m����m��ΪAC�ϵĵ㣨m��0��
��1���Էֱ����A��B��C��������ꣻ
��2�����P�˶���ʱ��Ϊt�룬�ʣ���tΪ��ֵʱ��DP��DB��ֱ����ȣ���˵�����ɣ�
��3����ͼ2����PA=AB���ڵ�����������һ����Q����QA��QB��QP���ҡ�PQA=60������Q�ڵ����������˶�ʱ�����APQ���PBQ�Ķ����ͣ�
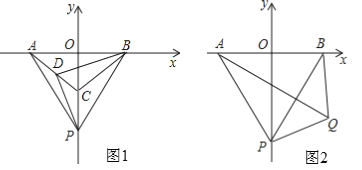
���𰸡���1��A����3��0����B��3��0����C��0����3������2����t=3��ʱ�� DP��DB��ֱ����ȣ����ɼ���������3����APQ+��PBQ=120�㣮
��������
��1������OA=OB=OC����AOC=��BOC=90�� �ó���ACB=90������������ABC�����Ϊ9���ó�OA=OC=OB=3 ���ɵó���������ꣻ
��2����DM��x���ڵ�M����DN��y���ڵ�N�������D������꣬�����ó���PCD�ա�BOD�������õ���BDP=��ODC=90������DP��DB��
��3����QA�Ͻ�ȡQS=QP������PS�����á�PQA=60�����ó���QSP�ǵȱ������Σ������ó���APS�ա�BPQ���Ӷ��ó���APQ+��PBQ=��APQ+��PAS�ó��𰸣�
��1��A����3��0����B��3��0����C��0����3����
��2����t=3��ʱ�� DP��DB��ֱ����ȣ�
�������£�����OD����DM��x���ڵ�M����DN��y���ڵ�N��
��D����m����m����
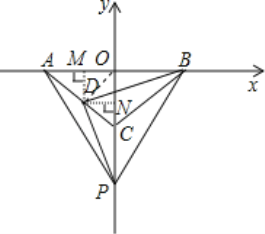
��DM=DN=OM=ON=m��
���DOM=��DON=45��������ACO=45�㣬
��DC=DO����ODC=90��
�ߡ�ODB+��BDC=��CDP+��BDC=90��
���ODB =��CDP
�� ��DP=DB
�� ��PCD�ա�BOD ��SAS��
��DP=DB����PDC=��BDO��
���BDP=��ODC=90�㣬
��DP��DB.
�� PC=BO
�� t=3 ��
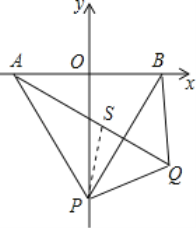
��3����QA�Ͻ�ȡQS=QP������PS��
�ߡ�PQA=60�㣬
���QSP�ǵȱ������Σ�
��PS=PQ����SPQ=60�㣬
��PO��AB�Ĵ�ֱƽ���ߣ�
��PA=PB ��PA=AB��
���PAB�ǵȱ������Σ�
���APB=60�㣬
���APS=��BPQ��
���APS�ա�BPQ��
���PAS=��PBQ��
���APQ+��PBQ=��APQ+��PAS=120�㣮