Question

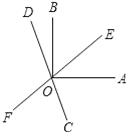
【题目】如图，直线EF，CD相交于点0，OA⊥OB，且OC平分∠AOF，

（1）若∠AOE=40°，求∠BOD的度数；

（2）若∠AOE=α，求∠BOD的度数；（用含α的代数式表示）

（3）从（1）（2）的结果中能看出∠AOE和∠BOD有何关系？

Answer 1

【答案】（1）20°；（2）α；（3）∠AOE=2∠BOD．

【解析】试题分析：（1）、（2）根据平角的性质求得∠AOF，又有角平分线的性质求得∠FOC；然后根据对顶角相等求得∠EOD=∠FOC；∠BOE=∠AOB﹣∠AOE，∠BOD=∠EOD﹣∠BOE；

（3）由（1）、（2）的结果找出它们之间的倍数关系．

试题解析：（1）∵∠AOE+∠AOF=180°（互为补角），∠AOE=40°，

∴∠AOF=140°；

又∵OC平分∠AOF，

∴∠FOC=∠AOF=70°，

∴∠EOD=∠FOC=70°（对顶角相等）；

而∠BOE=∠AOB﹣∠AOE=50°，

∴∠BOD=∠EOD﹣∠BOE=20°；

（2）∵∠AOE+∠AOF=180°（互为补角），∠AOE=α，

∴∠AOF=180°﹣α；

又∵OC平分∠AOF，

∴∠FOC=∠AOF=90°﹣α，

∴∠EOD=∠FOC=90°﹣α（对顶角相等）；

而∠BOE=∠AOB﹣∠AOE=90°﹣α，

∴∠BOD=∠EOD﹣∠BOE=α；

（3）从（1）（2）的结果中能看出∠AOE=2∠BOD．