题目内容
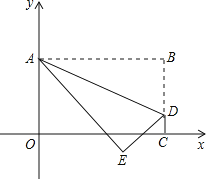
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 的解析式为
的解析式为![]() ,该直线与
,该直线与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() ,以
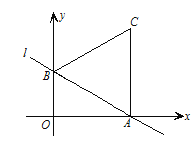
,以![]() 为边在第一象限内作正△ABC.若点
为边在第一象限内作正△ABC.若点![]() 在第一象限内,且满足
在第一象限内,且满足![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】分析:根据直线AB的解析式可求出A、B的坐标,此时可得出∠OBA=60°,那么AC∥y轴,因此C点的横坐标与A点的横坐标相同,C点的纵坐标是B点纵坐标的2倍据此可求出C点的坐标.由点![]() 在第一象限内,且满足
在第一象限内,且满足![]() ,得到P在过点C且与AB平行的直线l上.设直线l为y=﹣
,得到P在过点C且与AB平行的直线l上.设直线l为y=﹣![]() x+b,把C(
x+b,把C(![]() ,2)代入求得b的值,进而得出直线l的解析式,从而得出结论.
,2)代入求得b的值,进而得出直线l的解析式,从而得出结论.
详解:由直线y=﹣![]() x+1,求得点A的坐标为(
x+1,求得点A的坐标为(![]() ,0),点B的坐标为(0,1),∴在Rt△AOB中,OA=
,0),点B的坐标为(0,1),∴在Rt△AOB中,OA=![]() ,OB=1,∴AB=2,tan∠OBA=
,OB=1,∴AB=2,tan∠OBA=![]() ,
,
∴∠OBA=60°,∴∠OAB=90°﹣∠OBA=30°.
∵△ABC是等边三角形,∴CA=AB=2,∠CAB=60°,
∴∠CAD=∠CAB+∠OAB=90°,
∴点C的坐标为(![]() ,2).
,2).
∵S△AOB=![]() OB×OA=
OB×OA=![]() =
=![]() ,S△ABC=
,S△ABC=![]() =
=![]() ,又点
,又点![]() 在第一象限内,且满足
在第一象限内,且满足![]() ,∴P在过点C且与AB平行的直线l上.设直线l为y=﹣
,∴P在过点C且与AB平行的直线l上.设直线l为y=﹣![]() x+b,把C(
x+b,把C(![]() ,2)代入,得:-1+b=2,解得:b=3.∴直线l为y=﹣
,2)代入,得:-1+b=2,解得:b=3.∴直线l为y=﹣![]() x+3.
x+3.
∵点![]() 在第一象限内,故0<n<3.
在第一象限内,故0<n<3.
故选A.

 阅读快车系列答案
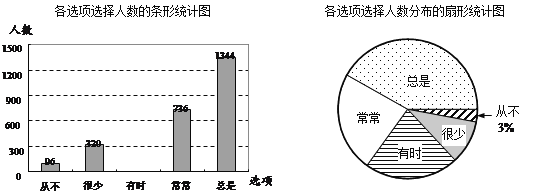
阅读快车系列答案【题目】在我市实施“城乡环境综合治理”期间,某校组织学生开展“走出校门,服务社会”的公益活动.八年级一班王浩根据本班同学参加这次活动的情况,制作了如下的统计图表:
该班学生参加各项服务的频数、频率统计表:
服务类别 | 频数 | 频率 |
文明宣传员 | 4 | 0.08 |
文明劝导员 | 10 | |
义务小警卫 | 8 | 0.16 |
环境小卫士 | 0.32 | |
小小活雷锋 | 12 | 0.24 |
请根据上面的统计图表,解答下列问题:

(1)该班参加这次公益活动的学生共有 名;
(2)请补全频数、频率统计表和频数分布直方图;
(3)若八年级共有900名学生报名参加了这次公益活动,试估计参加文明劝导的学生人数.
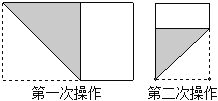
【题目】将图1中的正方形剪开得到图2,则图2中共有4个正方形;将图2中的一个正方形剪开得到图3,则图3中共有7个正方形;……如此剪下去,则第n个图形中正方形的个数是多少?

(1)将下表填写完整:
图(n) | 1 | 2 | 3 | 4 | 5 | …… | n |
正方形的个数 | 1 | 4 | 7 | …… | an |
(2)an= (用含n的代数式表示)
(3)按照上述方法,能否得到2019个正方形?如果能,请求出n;如果不能,请简述理由.