题目内容
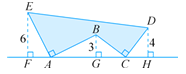
【题目】如图,AE⊥AB且AE=AB,BC⊥CD且BC=CD,请按图中所标注的数据,计算图中实线所围成的面积S是( )

A.50B.62C.65D.68
【答案】A
【解析】
由AE⊥AB,EF⊥FH,BG⊥AG,可以得到∠EAF=∠ABG,而AE=AB,∠EFA=∠AGB,由此可以证明△EFA≌△AGB,所以AF=BG,AG=EF;同理证得△BGC≌△CHD,GC=DH,CH=BG.故可求出FH的长,然后利用面积的割补法和面积公式即可求出图形的面积.
∵如图,AE⊥AB且AE=AB,EF⊥FH,BG⊥FH∠EAB=∠EFA=∠BGA=90,∠EAF+∠BAG=90,∠ABG+∠BAG=90∠EAF=∠ABG,
∴AE=AB,∠EFA=∠AGB,∠EAF=∠ABG△EFA≌△AGB,
∴AF=BG,AG=EF.
同理证得△BGC≌△CHD得GC=DH,CH=BG.
故FH=FA+AG+GC+CH=3+6+4+3=16
故S=![]() (6+4)×163×46×3=50.
(6+4)×163×46×3=50.
故选A.

练习册系列答案
相关题目
【题目】某商场用3300元购进节能灯100只,这两种节能灯的进价、售价如表:
进价(元/只) | 售价(元/只) | |
甲种节能灯 | 30 | 40 |
乙种节能灯 | 35 | 50 |
(1)求甲、乙两种节能灯各进多少只?
(2)全部售完100只节能灯后,该商场获利多少元?