题目内容
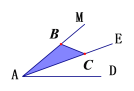
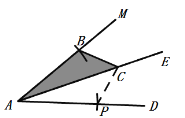
【题目】(1)如图,AE是∠MAD的平分线,点C是AE上一点,点B是AM上一点,在AD上求作一点P,使得△ABC≌△APC,请保留清晰的作图痕迹.
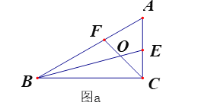
(2)如图a,在△ABC中, ∠ACB=![]() ,∠A=
,∠A=![]() ,BE、CF分别是∠ABC和∠ACB的角平分线,CF与BE相交于点O.请探究线段BC、BF、CE之间的关系,直接写出结论,不要求证明.
,BE、CF分别是∠ABC和∠ACB的角平分线,CF与BE相交于点O.请探究线段BC、BF、CE之间的关系,直接写出结论,不要求证明.
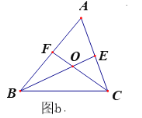
(3)如图b,若(2)中∠ACB为任意角,其它条件不变,请探究BC、BF、CE之间又有怎样的关系,请证明你的结论.
【答案】(1)答案见解析;(2)BC=BF+CE,证明见解析;(3)BC=BF+CE,证明见解析.
【解析】
(1)以点A为圆心,以AB长为半径画弧交AD于一点即可;
(2)在BC上截取BD=BF,首先证明△BFO≌△BDO,创造条件证明△COE≌△COD即可;
(3)在BC上截取BF'=BF,首先证明△BFO≌△BF'O,创造条件证明△COE≌△COF'即可.
(1)以点A为圆心,以AB长为半径画弧交AD于一点,则此点为所要求的点P.
(2)线段BC、BF、CE之间的关系为:BC=BF+CE .
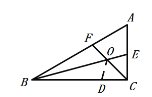
在BC上截取BD=BF.
在△BFO和△BDO中
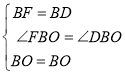
∴△BFO≌△BDO
∴∠BOF=∠BOD
∵∠A=![]() ,BE、CF分别是∠ABC和∠ACB的角平分线,CF与BE相交于点O.
,BE、CF分别是∠ABC和∠ACB的角平分线,CF与BE相交于点O.
∴∠BOC=180О-![]() ∠ABC-
∠ABC-![]() ∠ACB=180
∠ACB=180![]() -60
-60![]() =120
=120![]()
∴∠BOD=∠BOF=∠COE=180![]() -120
-120![]() =60
=60![]() .
.
∠COD=∠BOC-∠BOD=120![]() -60
-60![]() =60
=60![]()
在△COE和△COD中
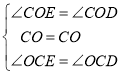
∴△COE≌△COD
∴CE=CD
∴BC=BF+CE .
(3)线段BC、BF、CE之间的关系为:BC=BF+CE .
在BC上截取BF'=BF.
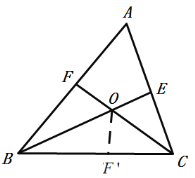
在△BFO和△BF'O中
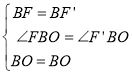
∴△BFO≌△BF'O
∴∠BOF=∠BOF'
∵∠A=60![]() ,BE、CF分别是∠ABC和∠ACB的角平分线,CF与BE相交于点O.
,BE、CF分别是∠ABC和∠ACB的角平分线,CF与BE相交于点O.
∴∠BOC=180О-![]() ∠ABC-
∠ABC-![]() ∠ACB=180
∠ACB=180![]() -60
-60![]() =120
=120![]()
∴∠BOF'=∠BOF=∠COE=180![]() -120
-120![]() =60
=60![]() .
.
∠COF'=∠BOC-∠BOF'=120![]() -60
-60![]() =60
=60![]()
在△COE和△COF'中
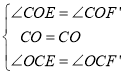
∴△COE≌△COF'
∴CE=CF'
∴BC=BF+CE .

 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案