题目内容
【题目】“和谐号”高铁列车的小桌板收起时可近似看作与地面垂直,展开小桌板使桌面保持水平,其示意图如图所示.连接OA,此时OA=75 cm,CB⊥AO,∠AOB=∠ACB=37°,且桌面宽OB与BC的长度之和等于OA的长度.求支架BC的长度(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75).

【答案】支架BC的长度约为37.5 cm.
【解析】
延长CB交AO于点D.则CD⊥OA,在Rt△OBD中根据正弦函数求得BD,根据余弦函数求得OD,在Rt△ACD中,根据正切函数求得AD,然后根据AD+OD=OA=75,列出关于x的方程,解方程即可求得.
延长CB交AO于点D,
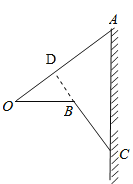
∴CD⊥OA.
设BC=x cm,则OB=(75-x)cm.
在Rt△OBD中,∵∠DOB=37°,
∴OD=OB·cos∠DOB≈0.8(75-x)=(60-0.8x)cm,BD=OB·sin∠DOB≈0.6(75-x)=(45-0.6x)cm,
∴DC=BD+BC≈(0.4+45x)cm.
在Rt△ACD中,∵∠ACD=37°,
∴AD=DC·tan∠ACD≈0.75(0.4x+45)=(0.3x+33.75)cm.
∵OA=AD+OD=75 cm,
∴0.3x+33.75+60-0.8x=75,
解得x≈37.5,
∴BC≈37.5 cm,
故支架BC的长度约为37.5 cm.

【题目】在学校组织的“文明出行”知识竞赛中,8(1)和8(2)班参赛人数相同,成绩分为A、B、C三个等级,其中相应等级的得分依次记为A级100分、B级90分、C级80分,达到B级以上(含B级)为优秀,其中8(2)班有2人达到A级,将两个班的成绩整理并绘制成如下的统计图,请解答下列问题:

(1)求各班参赛人数,并补全条形统计图;
(2)此次竞赛中8(2)班成绩为C级的人数为_______人;
(3)小明同学根据以上信息制作了如下统计表:
平均数(分) | 中位数(分) | 方差 | |
8(1)班 | m | 90 | n |
8(2)班 | 91 | 90 | 29 |
请分别求出m和n的值,并从优秀率和稳定性方面比较两个班的成绩;