题目内容
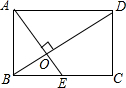
已知：矩形ABCD中，AB=1，点M在对角线AC上，直线l过点M且与AC垂直，与AD相交于点E．
（1）如果直线l与边BC相交于点H（如图1）AM=
AC且AD=a，求的AE长（用含a的代数式表示）；
（2）在（1）中，直线l把矩形分成两部分的面积比为2：5，求a的值；
（3）若AM=
AC，且直线l经过点B（如图2），求AD的长；
（4）如果直线l分别与边AD，AB相交于点E，F，AM=
AC，设AD的长为x，△AEF的面积为y，求y与x的函数关系式，并指出x的取值范围（求x的取值范围可不写过程）．
（1）如果直线l与边BC相交于点H（如图1）AM=
| 1 |
| 3 |
（2）在（1）中，直线l把矩形分成两部分的面积比为2：5，求a的值；
（3）若AM=
| 1 |
| 4 |
（4）如果直线l分别与边AD，AB相交于点E，F，AM=
| 1 |
| 4 |
（1）在Rt△ACD中，根据勾股定理有：AC2=AD2+DC2=a2+1
∵∠AME=∠D=90°，∠EAM=∠CAD
∴△AME∽△ADC，
∴
=
，
∴AE=
，
∵AM=
AC，
∴AE=
；
（2）∵AE∥BC，
∴△AEM∽△CHM，
∴
=
，
∵
=
，
∴
=
，即CH=2AE=
，
∴BH=a-CH=
，
∴
=
，
∴a2=
，即a=
；
（3）设AE=x，
∵AE∥BC，
∴
=
，
∵
=
，即
=
，
∴
=
，
设AE=x，则BC=3x，AC=
，
∵△AME∽△ADC，
∴
=
，
由于AM=
AC，AD=BC，
∴x•3x=
（1+9x2），
∴x=
，
∴AD=BC=3x=
；
（4）由题意可知：AC=
，AM=
，
∵△AEM∽△ACD
∴
=
，∴AE=
，
同理可得出
=
，
∴AF=
，
则S△AEF=
AE•AF=
（
≤x≤
）．
∵∠AME=∠D=90°，∠EAM=∠CAD
∴△AME∽△ADC，
∴
| AE |
| AC |
| AM |
| AD |
∴AE=
| AM•AC |
| AD |
∵AM=
| 1 |
| 3 |
∴AE=
| a2+1 |
| 3a |
（2）∵AE∥BC，
∴△AEM∽△CHM，
∴
| AE |
| CH |
| AM |
| MC |
∵
| AM |
| AC |
| 1 |
| 3 |
∴
| AE |
| CH |
| 1 |
| 2 |
| 2a2+2 |
| 3a |
∴BH=a-CH=
| a2-2 |
| 3a |
∴
| AE+BH |
| a-AE+a-BH |
| 2 |
| 5 |
∴a2=
| 7 |
| 2 |
| ||
| 2 |
（3）设AE=x，
∵AE∥BC，
∴
| AM |
| MC |
| AE |
| BC |
∵
| AM |
| AC |
| 1 |
| 4 |
| AM |
| MC |
| 1 |
| 3 |
∴
| AE |
| BC |
| 1 |
| 3 |
设AE=x，则BC=3x，AC=
| 1+9x2 |
∵△AME∽△ADC，
∴
| AE |
| AC |
| AM |
| AD |
由于AM=
| 1 |
| 4 |
∴x•3x=
| 1 |
| 4 |
∴x=
| ||
| 3 |
∴AD=BC=3x=
| 3 |
（4）由题意可知：AC=
| 1+x2 |
| 1 |
| 4 |
| 1+x2 |
∵△AEM∽△ACD
∴
| AE |
| AC |
| AM |
| AD |
| x2+1 |
| 4x |
同理可得出
| AF |
| AD |
| AE |
| DC |
∴AF=
| x2+1 |
| 4 |
则S△AEF=
| 1 |
| 2 |
| (x2+1)2 |
| 32x |
| ||
| 3 |
| 3 |
练习册系列答案
名题训练系列答案
期末集结号系列答案
相关题目
