[题目]已知.在河的两岸有A.B两个村庄.河宽为4千米.A.B两村庄的直线距离 AB=10千米.A.B两村庄到河岸的距离分别为1千米.3千米.计划在河上修建一座桥MN垂直于两岸.M点为靠近A村庄的河岸上一点.求AM+BN的最小值. 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】已知，在河的两岸有A，B两个村庄，河宽为4千米，A、B两村庄的直线距离 AB=10千米，A、B两村庄到河岸的距离分别为1千米、3千米，计划在河上修建一座桥MN垂直于两岸，M点为靠近A村庄的河岸上一点，求AM+BN的最小值.

【答案】 .

【解析】作BB'垂直于河岸，使BB′等于河宽，连接AB′，与靠近A的河岸相交于M，作MN垂直于另一条河岸，则MN∥BB′且MN=BB′，于是MNBB′为平行四边形，故MB′=BN；根据“两点之间线段最短”，AB′最短，即AM+BN最短，此时AM+BN=AB′．

作BB`垂直于河岸，使BB`等于河宽，连接AB`，与靠近A的河岸相交于M，作MN垂直于另一条河岸，

则MN∥BB`且MN=BB`，于是MNBB`为平行四边形，

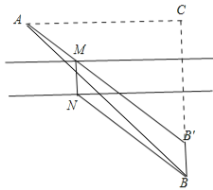
故MB`=BN，

当AM+MB′=AB时，AM+BN最小，

∵AB=10，BC=1+3+4=8，

∴在Rt△ABC中，，

在Rt△AB`C中，B`C=1+3+4千米，

∴ .

练习册系列答案

（1）求证：△AEB≌△CFD；

（2）连接AF，CE，若∠AFE=∠CFE，求证：四边形AFCE是菱形．

【题目】如图，一条抛物线与x轴相交于A、B两点，其顶点P在折线C﹣D﹣E上移动，若点C、D、E的坐标分别为（﹣1，4）、（3，4）、（3，1），点B的横坐标的最小值为1，则点A的横坐标的最大值为（）

A.1
B.2
C.3
D.4

【题目】化简求值：

（1）当a=﹣1，b=2时，求代数式﹣2（ab﹣3b2）﹣[6b2﹣（ab﹣a2）]的值

（2）先化简，再求值：4xy﹣2（x2﹣3xy+2y2）+3（x2﹣2xy），当（x﹣3）2+|y+1|=0，求式子的值

（3）若（2mx2﹣x+3）﹣（3x2﹣x﹣4）的结果与x的取值无关，求m的值

【题目】已知二次函数y=ax2+bx+1（a＜0）的图象过点（1，0）和（x1 ， 0），且﹣2＜x1＜﹣1，下列5个判断中：①b＜0；②b﹣a＜0；③a＞b﹣1；④a＜﹣ ；⑤2a＜b+ ，正确的是（）
A.①③
B.①②③
C.①②③⑤
D.①③④⑤

【题目】某商场服装部为了调动营业员的积极性，决定实行目标管理，根据目标完成的情况对营业员进行适当的奖励．为了确定一个适当的月销售目标，商场服装部统计了每个营业员在某月的销售额（单位：万元），数据如下：

17 18 16 13 24 15 28 26 18 19

22 17 16 19 32 30 16 14 15 26

15 32 23 17 15 15 28 28 16 19

（1）补全条形图；

（2）月销售额为　　的人数最多；

（3）如果想让一半左右的营业员都能达到销售目标，月销售目标定为多少合适？　　

A.15万元 B.16万元 C.18万元 D.19万元

（4）如果想确定一个较高的销售目标，你认为月销售目标定为多少合适？请说明理由．

【题目】爱好思考的小茜在探究两条直线的位置关系查阅资料时，发现了“中垂三角形”，即两条中线互相垂直的三角形称为“中垂三角形”．如图（1）、图（2）、图（3）中，AM、BN是△ABC的中线，AM⊥BN于点P，像△ABC这样的三角形均为“中垂三角形”．设BC=a，AC=b，AB=c．

（1）如图1，当tan∠PAB=1，c=4 时，a= ， b=；
如图2，当∠PAB=30°，c=2时，a= ， b=；
（2）请你观察（1）中的计算结果，猜想a2、b2、c2三者之间的关系，用等式表示出来，并利用图3证明你的结论．
（3）如图4，ABCD中，E、F分别是AD、BC的三等分点，且AD=3AE，BC=3BF，连接AF、BE、CE，且BE⊥CE于E，AF与BE相交点G，AD=3 ，AB=3，求AF的长．

【题目】（1）如图（1），已知：在△ABC中，∠BAC＝90°，AB=AC，直线m经过点A，BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.

（2）如图（2），将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=,其中为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.

（3）拓展与应用：如图（3），D、E是D、A、E三点所在直线m上的两动点（D、A、E三点互不重合）,点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形，连接BD、CE,若∠BDA=∠AEC=∠BAC，试判断△DEF的形状.

【题目】在《九章算术》中有求三角形面积公式“底乘高的一半”，但是在实际丈量土地面积时，量出高并非易事，所以古人想到了能否利用三角形的三条边长来求面积．我国南宋著名的数学家秦九韶（年—年）提出了“三斜求积术”，阐述了利用三角形三边长求三角形面积方法，简称秦九韶公式．在海伦（公元年左右，生平不详）的著作《测地术》中也记录了利用三角形三边长求三角形面积的方法，相传这个公式最早是由古希腊数学家阿基米德（公元前年—公元前年）得出的，故我国称这个公式为海伦一秦九韶公式．它的表达为：三角形三边长分别为、、，则三角形的面积（公式里的为半周长即周长的一半）．