题目内容
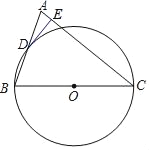
【题目】已知:如图,在△ABC中,AC=BC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
(1)求证:点D是AB的中点;
(2)求证:DE是⊙O的切线;
(3)若⊙O的直径为18,cosB=![]() ,求DE的长.
,求DE的长.
【答案】(1)见解析;(2)见解析;(3)4![]() .
.
【解析】
(1)连接CD,由BC为直径可知CD⊥AB,又BC=AC,由等腰三角形的底边“三线合一”证明结论;
(2)连接OD,则OD为△ABC的中位线,OD∥AC,已知DE⊥AC,可证DE⊥OC,证明结论;
(3)连接CD,在Rt△BCD中,已知BC=18,cosB=![]() ,求得BD=6,则AD=BD=6,在Rt△ADE中,已知AD=6,cosA=cosB=
,求得BD=6,则AD=BD=6,在Rt△ADE中,已知AD=6,cosA=cosB=![]() ,可求AE,利用勾股定理求DE.
,可求AE,利用勾股定理求DE.
(1)证明:连接CD,

∵BC是⊙O的直径,
∴CD⊥AB,又∵AC=BC,
∴AD=BD,
∴点D是AB的中点;
(2)证明:连接OD,
∵BD=DA,BO=OC,
∴DO是△ABC的中位线,
∴DO∥AC,
又∵DE⊥AC,
∴DE⊥DO,即DE是⊙O的切线;
(3)∵AC=BC,
∴∠B=∠A,
∴cos∠B=cos∠A=![]() ,
,
∵cos∠B=![]() =
=![]() ,BC=18,
,BC=18,
∴BD=6,
∴AD=6,
∵cos∠A=![]() =
=![]() ,
,
∴AE=2,
在Rt△AED中,DE=![]() =4
=4![]() .
.

 导学全程练创优训练系列答案
导学全程练创优训练系列答案【题目】小明在某一次实验中,测得两个变量之间的关系如下表所示:
自变量x | 1 | 2 | 3 | 4 | 12 | |
因变量y | 12.03 | 5.98 | 3.04 | 1.99 | 1.00 |
请你根据表格回答下列问题:
① 这两个变量之间可能是怎样的函数关系?你是怎样作出判断的?请你简要说明理由。
②请你写出这个函数的解析式。
③表格中空缺的数值可能是多少?请你给出合理的数值。
【题目】我市某中学开展“社会主义核心价值观”演讲比赛活动,九(1)、九(2)班根据初赛成绩各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.根据图中数据解决下列问题:

(1)根据图示求出表中的![]() 、
、![]() 、
、![]()
平均数 | 中位数 | 众数 | |
九(1) |
| 85 |
|
九(2) | 85 |
| 100 |
![]() ,
,![]() ,
,![]() .
.
(2)小明同学已经算出了九(2)班复赛成绩的方差:
![]() ,请你求出九(1)班复赛成绩的方差
,请你求出九(1)班复赛成绩的方差![]() ;
;
(3)根据(1)、(2)中计算结果,分析哪个班级的复赛成绩较好?