题目内容
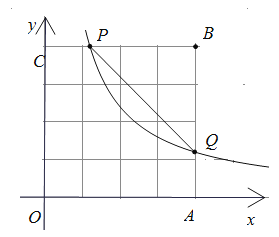
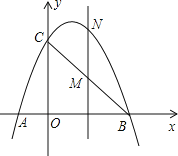
【题目】如图，已知抛物线经过点A（﹣1，0）、B（3，0）、C（0，3）三点．
（1）求抛物线的解析式．
（2）点M是线段BC上的点（不与B，C重合），过M作MN∥y轴交抛物线于N，若点M的横坐标为m，请用m的代数式表示MN的长．
（3）在（2）的条件下，连接NB、NC，是否存在m，使△BNC的面积最大？若存在，求m的值；若不存在，说明理由．
【答案】（1）y＝﹣x2+2x+3；（2）﹣m2+3m（0＜m＜3）；（3）最大值为
【解析】
（1）直接利用待定系数法即可求出抛物线的解析式；
（2）先利用待定系数法求出直线BC的解析式，已知点M的横坐标，代入直线BC、抛物线的解析式中，可得到M、N点的坐标，N、M纵坐标的差的绝对值即为MN的长；
（3）根据题（1）（2）的结论，列出SΔBNC关于m的表达式，再利用函数的性质求解SΔBNC的最大值即可．
解：（1）设抛物线的解析式为：y＝a（x+1）（x﹣3），则：
a（0+1）（0﹣3）＝3，a＝﹣1；
∴抛物线的解析式：y＝﹣（x+1）（x﹣3）＝﹣x2+2x+3；
（2）设直线BC的解析式为：y＝kx+b，则有：
，
解得
，
故直线BC的解析式：y＝﹣x+3．
已知点M的横坐标为m，MN∥y，则M（m，﹣m+3）、N（m，﹣m2+2m+3），
∴故MN＝﹣m2+2m+3﹣（﹣m+3）＝﹣m2+3m（0＜m＜3）；
（3）如图，
∵S△BNC＝S△MNC+S△MNB＝
MN（OD+DB）＝MNOB，
∴S△BNC＝（﹣m2+3m）3＝﹣
（m﹣）2+（0＜m＜3）；
∴当m＝时，△BNC的面积最大，最大值为．
【题目】欧拉（Euler，1707年~1783年）为世界著名的数学家、自然科学家，他在数学、物理、建筑、航海等领域都做出了杰出的贡献．他对多面体做过研究，发现多面体的顶点数（Vertex）、棱数E（Edge）、面数F（Flat surface）之间存在一定的数量关系，给出了著名的欧拉公式．
（1）观察下列多面体，并把下表补充完整：
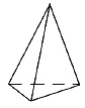
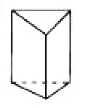
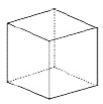
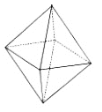
名称 | 三棱锥 | 三棱柱 | 正方体 | 正八面体 |
图形 |
|
|
|
|
顶点数V | 4 | 6 | 8 | |
棱数E | 6 | 12 | ||
面数F | 4 | 5 | 8 |
（2）分析表中的数据，你能发现V、E、F之间有什么关系吗？请写出关系式：____________________________．
