题目内容
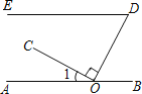
【题目】如图所示，点O在直线AB上，OC⊥OD，∠EDO与∠1互余，OF平分∠COD交DE于点F，若∠OFD=70°，求∠1的度数．
（1）使用直尺和圆规，补全图形；（保留作图痕迹）．
（2）解∵∠EDO与∠1互余
∴∠EDO+∠1=90°
∵OC⊥OD
∴∠COD=90°
∴∠EDO+∠1+∠COD=180°
∴______+______=180°
∴ED∥AB．（______）
∴∠AOF=∠OFD=70°（______）
∵OF平分∠COD，（已知）
∴∠COF=
∠COD=45°（______）
∴∠1=∠AOF-∠COF=______°．
【答案】（1）见解析；（2）∠EDO，∠AOD，同旁内角互补，两直线平行；两直线平行，内错角相等；角平分线的定义，25
【解析】
（1）依据OF平分∠COD交DE于点F，进行作图即可；
（2）依据同旁内角互补，两直线平行，判定ED∥AB，再根据平行线的性质以及角平分线的定义，即可得到∠1的度数．
解：（1）如图所示，OF平分∠COD交DE于点F，
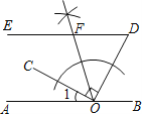
（2）∵∠EDO与∠1互余，
∴∠EDO+∠1=90°，
∵OC⊥OD，
∴∠COD=90°，
∴∠EDO+∠1+∠COD=180°，
∴∠EDO+∠AOD=180°，
∴ED∥AB，（同旁内角互补，两直线平行）
∴∠AOF=∠OFD=70°，（两直线平行，内错角相等）
∵OF平分∠COD，（已知）
∴∠COF=
∠COD=45°，（角平分线的定义）
∴∠1=∠AOF-∠COF=25°．
故答案为：∠EDO，∠AOD，同旁内角互补，两直线平行；两直线平行，内错角相等；角平分线的定义，25．
练习册系列答案
备战中考寒假系列答案
相关题目
