题目内容
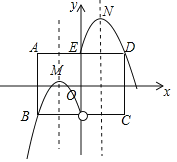
【题目】如图,在平面直角坐标系中,矩形ABCD的对称中心为坐标原点O,AD⊥y轴于点E(点A在点D的左侧),经过E、D两点的函数y=﹣![]() x2+mx+1(x≥0)的图象记为G1,函数y=﹣
x2+mx+1(x≥0)的图象记为G1,函数y=﹣![]() x2﹣mx﹣1(x<0)的图象记为G2,其中m是常数,图象G1、G2合起来得到的图象记为G.设矩形ABCD的周长为L.
x2﹣mx﹣1(x<0)的图象记为G2,其中m是常数,图象G1、G2合起来得到的图象记为G.设矩形ABCD的周长为L.
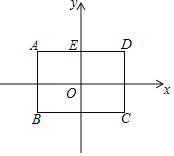
(1)当点A的横坐标为﹣1时,求m的值;
(2)求L与m之间的函数关系式;
(3)当G2与矩形ABCD恰好有两个公共点时,求L的值;
(4)设G在﹣4≤x≤2上最高点的纵坐标为y0,当![]() ≤y0≤9时,直接写出L的取值范围.
≤y0≤9时,直接写出L的取值范围.
【答案】(1)![]() ;(2)L=8m+4.(3)20;(4)12≤L≤44.
;(2)L=8m+4.(3)20;(4)12≤L≤44.
【解析】
(1)求出点B坐标利用待定系数法即可解决问题;
(2)利用对称轴公式,求出BE的长即可解决问题;
(3)由G2与矩形ABCD恰好有两个公共点,推出抛物线G2的顶点M(﹣m,![]() m2﹣1)在线段AE上,利用待定系数法即可解决问题;
m2﹣1)在线段AE上,利用待定系数法即可解决问题;
(4)分两种情形讨论求解即可.
(1)由题意E(0,1),A(﹣1,1),B(1,1)
把B(1,1)代入y=﹣![]() x2+mx+1中,得到1=﹣
x2+mx+1中,得到1=﹣![]() +m+1,
+m+1,
∴m=![]() ;
;
(2)∵抛物线G1的对称轴x=﹣![]() =m,
=m,
∴AE=ED=2m,
∵矩形ABCD的对称中心为坐标原点O,
∴AD=BC=4m,AB=CD=2,
∴L=8m+4;
(3)∵当G2与矩形ABCD恰好有两个公共点,
∴抛物线G2的顶点M(﹣m,![]() m2﹣1)在线段AE上,
m2﹣1)在线段AE上,
∴![]() m2﹣1=1,
m2﹣1=1,
∴m=2或﹣2(舍弃),
∴L=8×2+4=20;
(4)①当最高点是抛物线G1的顶点N(m,![]() m2+1)时,
m2+1)时,
若![]() m2+1=
m2+1=![]() ,解得m=1或﹣1(舍弃),
,解得m=1或﹣1(舍弃),
若![]() m2+1=9时,m=4或﹣4(舍弃),
m2+1=9时,m=4或﹣4(舍弃),
又∵m≤2,
观察图象可知满足条件的m的值为1≤m≤2,
②当(2,2m﹣1)是最高点时,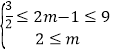 ,
,
解得2≤m≤5,
综上所述,1≤m≤5,
∴12≤L≤44.