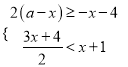题目内容
【题目】如图,把一根绳子对折成线段AB,从点P处把绳子剪断,已知AP:BP=2:3,若剪断后的各段绳子中最长的一段为60 cm,求绳子的原长.
![]()
【答案】(1)150cm (2)绳子的原长为150cm或100cm
【解析】
分点A和点B是对折点两种情况分别进行讨论,即可得出答案.
(1)当点A是绳子的对折点时,将绳子展开,如图①所示,
因为AP:BP=2:3,剪断后的各段绳子中最长的一段为60 cm,
所以2AP=60 cm,所以AP=30 cm,
所以BP=45 cm,
所以绳子的原长为2AB=2(AP+BP)=2×(30+45)=150(cm);
(2)当点B是绳子的对折点时,将绳子展开,如图②所示,
因为AP:BP=2:3,剪断后的各段绳子中最长的一段为60 cm,
所以2BP=60 cm,所以BP=30 cm,
所以AP=20 cm,
所以绳子的原长为2AB=2(AP+BP)=2×(20+30)=100(cm).
综上,绳子的原长为150 cm或100 cm..

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】我市某绿色无公害蔬菜基地有甲、乙两种植户,他们们种植了A、B两类蔬菜,两种植户种植的两类蔬菜的种植面积与总收入如下表:
种植户 | 种植A类蔬菜面积(单位:亩) | 种植B类蔬菜面积(单位:亩) | 总收入(单位:元) |
甲 | 1 | 3 | 13500 |
乙 | 2 | 2 | 13000 |
说明:不同种植户种植的同类蔬菜每亩平均收入相等
(1)求A、B两类蔬菜每亩平均收入各是多少元?
(2)今年甲、乙两种植户联合种植,计划合租50亩地用来种植A、B两类蔬菜,为了使总收入不低于16400元,问联合种植最多可以种植A类蔬菜多少亩?