题目内容
【题目】如图,抛物线y=ax2+bx+c过原点O、点A (2,﹣4)、点B (3,﹣3),与x轴交于点C,直线AB交x轴于点D,交y轴于点E.
(1)求抛物线的函数表达式和顶点坐标;
(2)直线AF⊥x轴,垂足为点F,AF上取一点G,使△GBA∽△AOD,求此时点G的坐标;
(3)过直线AF左侧的抛物线上点M作直线AB的垂线,垂足为点N,若∠BMN=∠OAF,求直线BM的函数表达式.
【答案】解:(1)∵将原点O、点B、点C的坐标代入得: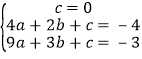 ,解得:a=1,b=﹣4,c=0,
,解得:a=1,b=﹣4,c=0,
∴抛物线的解析式为y=x2﹣4x.
(2)设直线AB的解析式为y=kx+b.
∵将点A(2,﹣4)、B(3,﹣3)代入得![]() ,解得:k=1,b=﹣6,
,解得:k=1,b=﹣6,
∴直线AB的解析式为y=x﹣6.
∵令y=0得x﹣6=0,解得:x=6,
∴D(6,0).
∴OD=6.
∵AF⊥x轴,(2,﹣4),
∴F(2,0).
∴AF=4,DF=4.
∴AF=DF.
∴∠GAB=∠ODA.
∴当![]() 时,△GBA∽△AOD.
时,△GBA∽△AOD.
∵由两点间的距离公式可知AB=![]() =
=![]() ,AD=
,AD=![]() =4
=4![]() ,
,
∴![]() ,解得;AG=
,解得;AG=![]() .
.
∴G(2,﹣![]() ).
).
(3)如图1所示:BM与AF的交点记为G.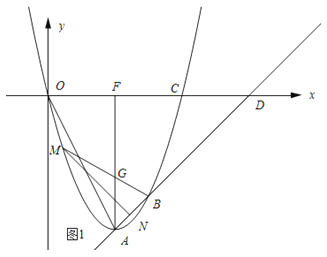
∵∠BMN=∠OAF,∠A=∠ODA,
∴△GBA∽△AOD.
∴![]() ,即
,即![]() ,解得;AG=
,解得;AG=![]() .
.
∴G(2,﹣![]() ).
).
设直线BM的解析式为y=kx+b.
∵将点B、G的坐标代入得: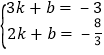 ,解得:k=﹣
,解得:k=﹣![]() ,b=﹣2.
,b=﹣2.
∴直线BM的解析式为y=﹣![]() X﹣2.
X﹣2.
如图2所示:MB与x交点记为G.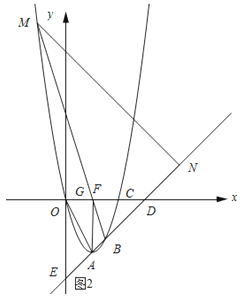
BD=AD﹣AB=4![]() ﹣
﹣![]() =3
=3![]() .
.
∵∠BMN=∠OAF,∠GDB=∠ODA,
∴△FBD∽△AOD.
∴![]() ,即
,即![]() ,解得DG=4.
,解得DG=4.
∴点G的坐标为(2,0).
设直线BM的解析式为y=kx+b.
∵将点B和点G的坐标代入得:![]() ,解得k=﹣3,b=6.
,解得k=﹣3,b=6.
∴直线BM的解析式为y=﹣3x+6.
综上所述,直线MB的解析式为y=-![]() x﹣2或y=﹣3x+6.
x﹣2或y=﹣3x+6.
【解析】(1)将原点O、点B、点C的坐标代入求得a、b、c的值即可;
(2)先求得直线AB的解析式,然后可求得点D的坐标,于是得到AF=DF,由两点间的距离公式可求得AB、AD的长,由等腰三角形的性质可证明∠GAB=∠ODA,故此![]() 时,△GBA∽△AOD.接下来依据关系式可求得AG的长,从而可求得点G的坐标;
时,△GBA∽△AOD.接下来依据关系式可求得AG的长,从而可求得点G的坐标;
(3)如图1所示:BM与AF的交点记为G.先证明△GBA∽△AOD,由相似三角形的性质可求得AG的长,于是得到点G的坐标,然后依据待定系数法可求得BM的解析式;如图2所示:MB与x交点记为G.先证明△FBD∽△AOD,由相似三角形的性质可求得DG的长,从而得到点G的坐标,然后依据待定系数法可求得MB的解析式

 全优点练单元计划系列答案
全优点练单元计划系列答案