题目内容
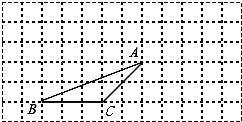
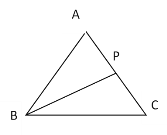
【题目】如图，在△ACB中，有一点P在AC上移动，若AB=AC=5，BC=6，则AP+BP+CP的最小值为（ ）
A.9.6B.9.8C.11D.10.2
【答案】B
【解析】
过点A作AD⊥BC于D，根据题意可得当BP最小时，AP+BP+CP最小，然后根据垂线段最短可得当BP⊥AC时，BP最小，然后根据三线合一和勾股定理即可求出BD和AD，然后根据S△ABC=
BC·AD=AC·BP即可求出此时的BP，从而求出结论．
解：过点A作AD⊥BC于D
∵AP＋CP=AC=5
∴AP+BP+CP=5＋BP，即当BP最小时，AP+BP+CP最小，
根据垂线段最短，当BP⊥AC时，BP最小
∵AB=AC=5，BC=6，
∴BD=BC=3
根据勾股定理AD=
=4
此时S△ABC=BC·AD=AC·BP
∴×6×4=×5·BP
解得：BP=
∴AP+BP+CP的最小值为＋5=
故选B．
练习册系列答案
开心蛙状元作业系列答案
课时掌控随堂练习系列答案
一课一练一本通系列答案
浙江之星学业水平测试系列答案
相关题目
【题目】谁更合理？
某种牙膏上部圆的直径为2.6cm，下部底边的长为4cm，如图，现要制作长方体的牙膏盒，牙膏盒底面是正方形，在手工课上，小明、小亮、小丽、小芳制作的牙膏盒的高度都一样，且高度符合要求．不同的是底面正方形的边长，他们制作的边长如下表：
制作者 | 小明 | 小亮 | 小丽 | 小芳 |
正方形的边长 | 2cm | 2.6cm | 3cm | 3.4cm |
（1）这4位同学制作的盒子都能装下这种牙膏吗？（
）
（2）若你是牙膏厂的厂长，从节约材料又方便取放牙膏的角度来看，你认为谁的制作更合理？并说明理由．
