��Ŀ����
����Ŀ����ͼ��������y=��x2��2x+3��ͼ����x�ύ��A��B���㣨��A�ڵ�B����ߣ�����y�ύ�ڵ�C����DΪ�����ߵĶ��㣮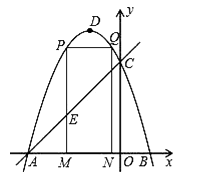
��1�����A��B��C�����ꣻ
��2����M��m��0��Ϊ�߶�AB��һ�㣨��M�����A��B�غϣ�������M��x��Ĵ��ߣ���ֱ��AC���ڵ�E���������߽��ڵ�P������P��PQ��AB���������ڵ�Q������Q��QN��x���ڵ�N���ɵþ���PQNM����ͼ����P�ڵ�Q��ߣ����ú�m��ʽ�ӱ�ʾ����PQNM���ܳ���
��3��������PQNM���ܳ����ʱ��m��ֵ�Ƕ��٣��������ʱ�ġ�AEM�������
��4���ڣ�3���������£�������PMNQ���ܳ����ʱ������DQ������������һ��F��y���ƽ���ߣ���ֱ��AC���ڵ�G����G�ڵ�F���Ϸ�������FG= ![]() DQ�����F�����꣮
DQ�����F�����꣮
���𰸡�
��1���⣺�������� ![]() ��֪��C��0��3����
��֪��C��0��3����
��y=0���� ![]() ��
��
���x=��3��x=1��
��A����3��0����B��1��0����
��2���⣺�������� ![]() ��֪���Գ���Ϊx=��1��
��֪���Գ���Ϊx=��1��
��M��ĺ�����Ϊm��
��PM= ![]() ��MN=����m��1����2=��2m��2��
��MN=����m��1����2=��2m��2��
�����PMNQ���ܳ�=2��PM+MN��=�� ![]() ����2=
����2= ![]() =
= ![]()
�൱m=��2ʱ���ε��ܳ����
��3���⣺�߾���PMNQ���ܳ�=2��PM+MN��=�� ![]() ����2=
����2= ![]() =
= ![]() �൱m=��2ʱ���ε��ܳ����
�൱m=��2ʱ���ε��ܳ����
��A����3��0����C��0��3������ֱ��AC����ʽΪy=kx+b�����k=1��b=3�������ʽy=x+3����x=��2ʱ����E����2��1������EM=1��AM=1����S= ![]() AMEM=
AMEM= ![]()
��4���⣺��M��ĺ�����Ϊ��2�������ߵĶԳ���Ϊx=��1����NӦ��ԭ���غϣ�Q����C���غϣ���DQ=DC����x=��1���� ![]() �����y=4����D����1��4������DQ=DC=
�����y=4����D����1��4������DQ=DC= ![]() ����FG=
����FG= ![]() DQ����FG=4����F��n��
DQ����FG=4����F��n�� ![]() ������G��n��n+3�����ߵ�G�ڵ�F���Ϸ�����
������G��n��n+3�����ߵ�G�ڵ�F���Ϸ����� ![]() =4����ã�n=��4��n=1����F����4����5����1��0����
=4����ã�n=��4��n=1����F����4����5����1��0����
����������1�����ú���ͼ����������Ľ�������������������A��B��C�����ꡣ
��2����ȷ���������߶Գ��ᣬ��M��ĺ�����Ϊm���ú�m��ʾ��PM��MN���ٸ��ݾ���PMNQ���ܳ�=2��PM+MN����������������ʽ�����ݶ��κ��������ʼ��ɵó������
��3���ɣ�2���õ��Ľ����жϳ������ܳ����ʱ��ȷ����m���������ֱ��AC����ʽ�������������ʱ�ġ�AEM�������
��4���ڣ�3���Ļ����ϣ��жϳ�NӦ��ԭ���غϣ�Q����C���غϣ����DQ=DC=![]() �����FG�ij������F�����꼰��G�����꣬����FG�ij�=4���������̣��ⷽ�����n��ֵ���Ϳ������F�����ꡣ
�����FG�ij������F�����꼰��G�����꣬����FG�ij�=4���������̣��ⷽ�����n��ֵ���Ϳ������F�����ꡣ

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�