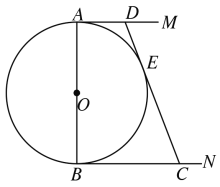
题目内容
【题目】如图,![]() 的直径
的直径![]() ,
,![]() ,
,![]() 是
是![]() 的两条切线,
的两条切线,![]() 切
切![]() 于
于![]() ,交
,交![]() 于
于![]() ,设
,设![]() ,
,![]() ,
,![]() .
.
(1)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)若![]() ,
,![]() 是
是![]() 的两实根,求
的两实根,求![]() ,
,![]() 的值;
的值;
(3)在(2)的前提下,求![]() 的面积.
的面积.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)45
;(3)45
【解析】
(1)作DF⊥BN交BC于F;根据切线长定理得到BF=AD=x,CE=CB=y,则DC=DE+CE=x+y,在直角△DFC中根据勾股定理,就可以求出y与x的关系;
(2)由(1)求得xy=36,然后由根与系数的关系求得a的值,通过解一元二次方程即可求得x、y的值;
(3)由AM,BN是圆 O的两条切线,DC切圆 O于E,得到OE⊥CD,AD=DE,BC=CE,利用三角形面积公式即可求解.
(1)如图,作DF⊥BN交BC于F;
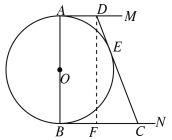
∵AM、BN与O切于点A、 B,
∴AB⊥AM,AB⊥BN.
又∵DF⊥BN,
∴∠BAD=∠ABC=∠BFD=90°,
∴四边形ABFD是矩形,
∴BF=AD=x,DF=AB=12,
∵BC=y,
∴FC=BCBF=yx;
∵DE切O于E,
∴DE=DA=x,CE=CB=y,
则DC=DE+CE=x+y,
在Rt△DFC中,
由勾股定理得:(x+y)2=(yx)2+122,
整理为:![]() ,
,
∴y与x的函数关系式是![]() .
.
(2)由(1)知xy=36,
x,y是方程2t230t+a=0的两个根,
∴根据韦达定理知,xy=![]() ,即a=72;
,即a=72;
∴原方程为t215t+36=0,
解得![]() 或
或![]()
∵x<y,
∴![]() ;
;
(3)如图,连接OD,OE,OC,
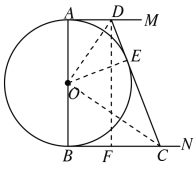
∵AD,BC,CD是圆O的切线,
∴OE⊥CD,AD=DE=3,BC=CE=12,
∴S△COD=![]()

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目