题目内容
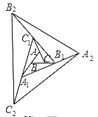
【题目】如图，若S△ABC=1分别倍长(延长一倍)AB、BC、CA得到
再分别延长
得到
……，按此规律，延长
次后得到的
的面积为_________.
【答案】
【解析】
试题先根据图形特征找出延长各边后得到的三角形的面积是原三角形的面积的倍数的规律，再利用发现的规律求延长第n次后的面积．
△AA1C=3△ABC=3，
△AA1C1=2△AA1C=6，
所以△A1B1C1=6×3+1=19；
同理得△A2B2C2=19×19=361；
△A3B3C3=361×19=6859，
△A4B4C4=6859×19=130321，
△A5B5C5=130321×19=2476099，
从中可以得出一个规律，延长各边后得到的三角形是原三角形的19倍，所以延长第n次后，得到△AnBnCn，
则其面积为．
练习册系列答案
相关题目
